摘要: (本题满分12分.第1小题4分.第2小题8分) 如图.已知点在圆柱的底面圆上. 为圆的直径. (1)求证:, (2)若圆柱的体积为.. .求异面直线与所成的角(用 反三角函数值表示结果).
网址:http://m.1010jiajiao.com/timu3_id_532308[举报]
(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分)
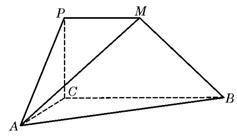 如图,
如图,![]() 是直角梯形,∠
是直角梯形,∠![]() =90°,
=90°,![]() ∥
∥![]() ,
,![]() =1,
=1,![]() =2,又
=2,又![]() =1,∠
=1,∠![]() =120°,
=120°,![]() ⊥
⊥![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分)
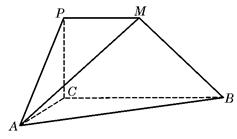 如图,
如图, 是直角梯形,∠
是直角梯形,∠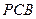 =90°,
=90°,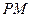 ∥
∥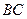 ,
,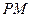 =1,
=1,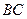 =2,又
=2,又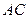 =1,∠
=1,∠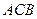 =120°,
=120°,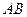 ⊥
⊥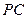 ,直线
,直线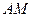 与直线
与直线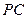 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面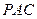 ⊥平面
⊥平面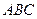 ;
;
(Ⅱ)求二面角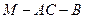 的大小;
的大小;
(Ⅲ)求三棱锥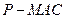 的体积.
的体积.
 如图,
如图, 是直角梯形,∠
是直角梯形,∠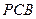 =90°,
=90°,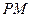 ∥
∥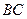 ,
,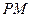 =1,
=1,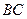 =2,又
=2,又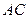 =1,∠
=1,∠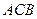 =120°,
=120°,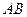 ⊥
⊥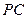 ,直线
,直线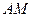 与直线
与直线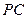 所成的角为60°.
所成的角为60°.(Ⅰ)求证:平面
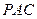 ⊥平面
⊥平面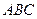 ;
;(Ⅱ)求二面角
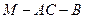 的大小;
的大小;(Ⅲ)求三棱锥
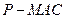 的体积.
的体积.(本题满分12分)
在高二年级某班学生在数学校本课程选课过程中,已知第一小组与第二小组各有六位同学.每位同学都只选了一个科目,第一小组选《数学运算》的有1人,选《数学解题思想与方法》的有5人,第二小组选《数学运算》的有2人,选《数学解题思想与方法》的有4人,现从第一、第二两小组各任选2人分析选课情况.
(Ⅰ)求选出的4 人均选《数学解题思想与方法》的概率;
(Ⅱ)设![]() 为选出的4个人中选《数学运算》的人数,求
为选出的4个人中选《数学运算》的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
 ,函数
,函数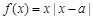 .
. 时,求使
时,求使 成立的
成立的 的集合;
的集合; 在区间
在区间 上的最小值.
上的最小值.