题目内容
(本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.
已知 ,函数
,函数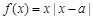 .
.
(Ⅰ)当 时,求使
时,求使 成立的
成立的 的集合;
的集合;
(Ⅱ)求函数 在区间
在区间 上的最小值.
上的最小值.
【答案】
(Ⅰ) ;
;
(Ⅱ)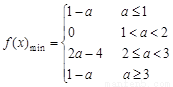 。
。
【解析】本试题主要是考查了分段函数的不等式的求解,以及不等式恒成立问题中最值的求解,以及二次函数的性质的综合运用。
(1)因为函数 .故当
.故当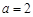 时,求使
时,求使 成立的
成立的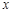 的集合,只需要对x分情况讨论既可以得到。
的集合,只需要对x分情况讨论既可以得到。
(2)要求函数 在区间
在区间 上的最小值,分析对称轴和定义域的关系,分类讨论得到结论。
上的最小值,分析对称轴和定义域的关系,分类讨论得到结论。
(Ⅰ)由题意, . …………………………………………1分
. …………………………………………1分
当 时,
时,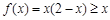 ,解得
,解得 ; ……………………………2分
; ……………………………2分
当 时,
时,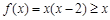 ,解得
,解得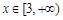 . ……………………………3分
. ……………………………3分
综上,所求解集为 ……………………………………………………4分
……………………………………………………4分
(Ⅱ)①当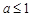 时,在区间
时,在区间 上,
上,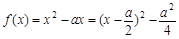 ,其图像是开口向上的抛物线,对称轴是
,其图像是开口向上的抛物线,对称轴是 ,
,
∵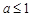 ,
,
∴ ,
,
∴ ……………………………………………………6分
……………………………………………………6分
② 当 时,在区间[1,2]上,
时,在区间[1,2]上,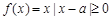 ,
, ……8分
……8分
③当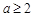 时,在区间[1,2]上,
时,在区间[1,2]上, ,其图像是开口向下的抛物线,对称轴是
,其图像是开口向下的抛物线,对称轴是 ,
,
 当
当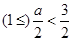 即
即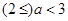 时,
时, …………10分
…………10分
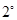 当
当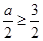 即
即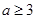 时,
时,
∴综上,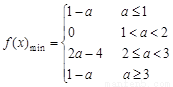 …………………………………………12分
…………………………………………12分

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 ,
, ,…,
,…,  后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率;
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 中, AD=2,AB=AD=4,
中, AD=2,AB=AD=4, ,点E是AB的中点,点F是
,点E是AB的中点,点F是 的中点。
的中点。  ;
;  与
与 所成的角的大小;
所成的角的大小;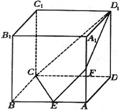
 ,且以下命题都为真命题:
,且以下命题都为真命题: 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数; 存在复数
存在复数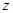 同时满足
同时满足 且
且 .
.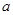 的取值范围.
的取值范围.