题目内容
(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分)
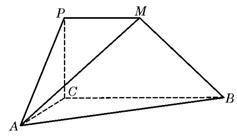 如图,
如图,![]() 是直角梯形,∠
是直角梯形,∠![]() =90°,
=90°,![]() ∥
∥![]() ,
,![]() =1,
=1,![]() =2,又
=2,又![]() =1,∠
=1,∠![]() =120°,
=120°,![]() ⊥
⊥![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
(Ⅰ)略 (Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
解法一:
(Ⅰ)∵![]()
∴![]() ,又∵
,又∵![]() ∴
∴![]() …(4分)
…(4分)
(Ⅱ)取![]() 的中点
的中点![]() ,则
,则![]() ,连结
,连结![]() ,
,
∵![]() ,∴
,∴![]() ,从而
,从而![]()
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() ,则由三垂线定理知,
,则由三垂线定理知,![]() ,
,
从而![]() 为二面角
为二面角![]() 的平面角
的平面角
直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ∴
∴![]()
在![]() 中,由余弦定理得
中,由余弦定理得![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,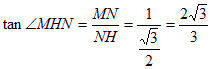
故二面角![]() 的平面角大小为
的平面角大小为![]() …(9分)
…(9分)
(Ⅲ)由(Ⅱ)知,![]() 为正方形
为正方形
∴![]() ……(12分)
……(12分)
解法二:(Ⅰ)同解法一…(4分)
(Ⅱ)在平面![]() 内,过
内,过![]() 作
作![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() (如图)
(如图)
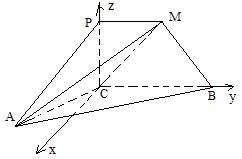 由题意有
由题意有![]() ,设
,设![]() ,
,
则![]()
由直线![]() 与直线
与直线![]() 所成的解为
所成的解为![]() ,得
,得
![]() ,即
,即![]() ,解得
,解得![]()
∴![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则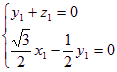 ,取
,取![]() ,得
,得![]()
平面![]() 的法向量取为
的法向量取为![]() ,设
,设![]() 与
与![]() 所成的角为
所成的角为![]() ,则
,则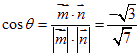
显然,二面角![]() 的平面角为锐角,故二面角
的平面角为锐角,故二面角![]() 的平面角大小为
的平面角大小为![]()
(Ⅲ)取平面![]() 的法向量取为
的法向量取为![]() ,则点A到平面
,则点A到平面![]() 的距离
的距离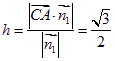
∵![]() ,∴
,∴![]() …(12分)
…(12分)

练习册系列答案
相关题目
 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。 ,求实数
,求实数 的取值范围。
的取值范围。 是棱
是棱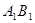 的中点,
的中点,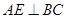 ;
; 与平面
与平面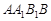 所成角大小(用反三角函数表示).
所成角大小(用反三角函数表示).