摘要: a与b的数量积的概念 已知两个非零向量a和b.它们的夹角为θ.则数量|a||b|cosθ叫做a与b的数量积.记作a·b. 注意:(1)a与b的数量积的结果是一个实数.
网址:http://m.1010jiajiao.com/timu3_id_527259[举报]
已知F1、F2是双曲线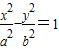 的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,
的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,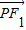 与
与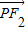 的数量积
的数量积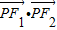 的最小值是-16.
的最小值是-16.
(1)求双曲线的方程;
(2)过点C(9,16)能否作直线l与双曲线交于A、B两点,使C为线段AB的中点.若能,求出直线l的方程;若不能,说明理由.
查看习题详情和答案>>
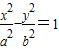 的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,
的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,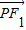 与
与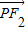 的数量积
的数量积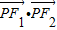 的最小值是-16.
的最小值是-16.(1)求双曲线的方程;
(2)过点C(9,16)能否作直线l与双曲线交于A、B两点,使C为线段AB的中点.若能,求出直线l的方程;若不能,说明理由.
查看习题详情和答案>>
已知向量a,b满足关系式![]() |a-λb|=|λa+b|(λ>0),且a=(cosα,sinα),b=(-
|a-λb|=|λa+b|(λ>0),且a=(cosα,sinα),b=(-![]() ,
,![]() ).
).
(1)试用λ表示向量a与b的数量积;
(2)求a与b所夹锐角的最大值,并求此时λ的值.
已知F1、F2是双曲线![]() 的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,
的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,![]() 与
与![]() 的数量积
的数量积![]() 的最小值是-16.
的最小值是-16.
(1)求双曲线的方程;
(2)过点C(9,16)能否作直线l与双曲线交于A、B两点,使C为线段AB的中点.若能,求出直线l的方程;若不能,说明理由.