题目内容
已知F1、F2是双曲线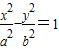 的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,
的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,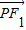 与
与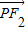 的数量积
的数量积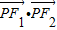 的最小值是-16.
的最小值是-16.(1)求双曲线的方程;
(2)过点C(9,16)能否作直线l与双曲线交于A、B两点,使C为线段AB的中点.若能,求出直线l的方程;若不能,说明理由.
【答案】分析:(1))由|PF1|=ex+a≥e•a+a=c+a,得a+c=8①,消掉y可得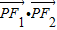 的最小值,令其为-16②,结合a2+b2=c2可得a,b;
的最小值,令其为-16②,结合a2+b2=c2可得a,b;
(2)平方差法:假设存在这样的直线满足题条件,设A(x1,y1),B(x2,y2)代入双曲线方程并作差,可得直线AB的斜率k,从而可得直线l的方程,然后联立直线与双曲线的方程消掉y可得△>0,从而得到结论;
解答:解:(1)∵|PF1|=ex+a≥e•a+a=c+a,当且仅当x=a时,等号取得,
∴|PA|的最小值为c+a,∴c+a=8①,
∴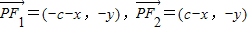 ,
,
由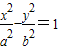 知
知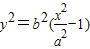 ,
,
∴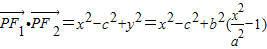 =
=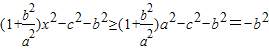 ,
,
∴当且仅当x=a时,等号取得,
∴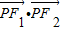 的最小值为-b2,∴b2=16,即b=4②,
的最小值为-b2,∴b2=16,即b=4②,
又∵c2=a2+b2③
∴由①②③得a=3,b=4,c=5
∴所求双曲线的方程为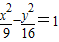 ;
;
(2)假设存在这样的直线满足题条件,设A(x1,y1),B(x2,y2)
则有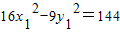 ④,
④,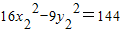 ⑤,
⑤,
④-⑤得16(x1+x2)(x1-x2)-9(y1+y2)(y1-y2)=0,
则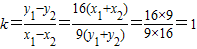 ,
,
∴直线l的方程为y-x=7,
将直线l:y-x=7与双曲线16x2-9y2=144组成方程组消去y,得7x2-126x-585=0,其根的判别式△>0,
∴这样的直线l存在,方程为x-y+7=0;
点评:本题考查直线与圆锥曲线的位置关系、双曲线的方程和性质,涉及弦中点问题往往运用平方差法.
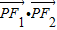 的最小值,令其为-16②,结合a2+b2=c2可得a,b;
的最小值,令其为-16②,结合a2+b2=c2可得a,b;(2)平方差法:假设存在这样的直线满足题条件,设A(x1,y1),B(x2,y2)代入双曲线方程并作差,可得直线AB的斜率k,从而可得直线l的方程,然后联立直线与双曲线的方程消掉y可得△>0,从而得到结论;
解答:解:(1)∵|PF1|=ex+a≥e•a+a=c+a,当且仅当x=a时,等号取得,
∴|PA|的最小值为c+a,∴c+a=8①,
∴
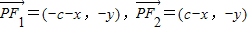 ,
,由
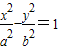 知
知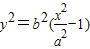 ,
,∴
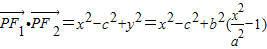 =
=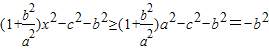 ,
,∴当且仅当x=a时,等号取得,
∴
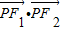 的最小值为-b2,∴b2=16,即b=4②,
的最小值为-b2,∴b2=16,即b=4②,又∵c2=a2+b2③
∴由①②③得a=3,b=4,c=5
∴所求双曲线的方程为
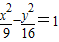 ;
;(2)假设存在这样的直线满足题条件,设A(x1,y1),B(x2,y2)
则有
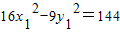 ④,
④,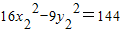 ⑤,
⑤,④-⑤得16(x1+x2)(x1-x2)-9(y1+y2)(y1-y2)=0,
则
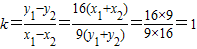 ,
,∴直线l的方程为y-x=7,
将直线l:y-x=7与双曲线16x2-9y2=144组成方程组消去y,得7x2-126x-585=0,其根的判别式△>0,
∴这样的直线l存在,方程为x-y+7=0;
点评:本题考查直线与圆锥曲线的位置关系、双曲线的方程和性质,涉及弦中点问题往往运用平方差法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
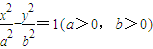 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若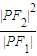 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )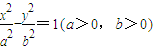 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若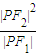 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )