摘要：20．已知函数在(1.2是增函数. 在(0.1)为减函数. (Ⅰ)求.的表达式, (Ⅱ)求证:当时.方程有唯一解. 21．在△ABC中.sinA.sinB.sinC构成公差为正的等差数列.且其周长为12.以为x轴.AC的中垂线为y轴建立直角坐标系xoy. (Ⅰ)证明存在两个定点E.F.使得|BE|+|BF|为定长, 并求出点E.F的坐标及点B的轨迹Γ, (Ⅱ)设P为轨迹Γ上的任一点.点M.N分别在射线 PA.PC上.动点Q满足. 经过点A且以为方向向量的直线与动 点Q的轨迹交于点R.试问:是否存在一个定点D. 使得为定值?若存在.求出点D的坐标,若不存在.说明理由?
网址：http://m.1010jiajiao.com/timu3_id_524125[举报]
(本小题满分12分)
已知函数
在
处的切线方程为
,
（1）若函数
在
时有极值,求
的表达式;
（2）在(1)条件下,若函数
在
上的值域为
,求m的取值范围;
(3) 若函数在区间
上单调递增，求b的取值范围.
查看习题详情和答案>>
在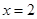
时取得极值.
满足的关系式； （2）当
时，求函数
的单调递增区间.
（1）若函数
存在单调递减区间，求
的取值范围；（2）若
且关于x的方程
在
上恰有两个不相等的实数根，求实数
的取值范围；
,
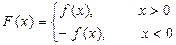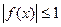在区间(0,1]上恒成立，试求b的取值范围。
函数f (x)=
x3+ ax2－bx (a, b∈R) .
)处的切线斜率为－4
，求y=f (x)的极大值；