题目内容
(本小题满分12分) 已知函数f(x)=ax2+bx+c(a>0,b∈R, c∈R).
(Ⅰ)若函数f(x)的最小值是f(-1)=0,且c=1,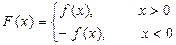
,
求F(2)+F(-2)的值
(Ⅱ)若a=1,c=0,且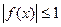
在区间(0,1]上恒成立，试求b的取值范围。
解：（1）由已知：c=1,a-b+c=0,-b/2a=-1,,a=1,b=2,f(x)=(x+1)2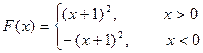
F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8
（2）
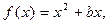原命题等价于
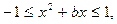在区间(0,1]上恒成立
即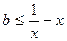
且
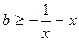在区间(0,1]上恒成立。又
的最小值为0，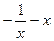
的最大值为-2，∴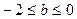
解析
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
