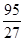题目内容
(本小题满分12分)
已知函数 在
在 处的切线方程为
处的切线方程为
 ,
,
(1)若函数 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)条件下,若函数 在
在 上的值域为
上的值域为 ,求m的取值范围;
,求m的取值范围;
(3) 若函数 在区间
在区间 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
【答案】
由 求导得
求导得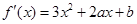 ,
,
由已知切线方程为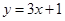 ,故f′(1)=3,,f(1)=4,
,故f′(1)=3,,f(1)=4,
所以
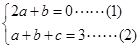

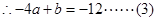
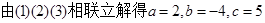
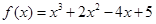 …………4分
…………4分
(2)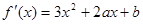 =
=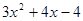 =
=
|
x |
-2 |
(-2, |
|
( |
|
|
0 |
- |
0 |
+ |
|
f(x) |
13 |
|
|
|
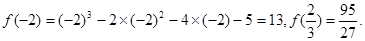
当x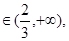 令
令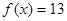 得x=2,由题意得m的取值范围为
得x=2,由题意得m的取值范围为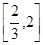 .………………9分
.………………9分
(3)y=f(x)在区间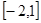 上单调递增,
上单调递增,
又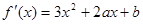 ,由(1)知2a+b=0,
,由(1)知2a+b=0,
∴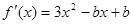 .
.
依题意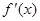 在[-2,1]恒有
在[-2,1]恒有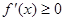 ,即
,即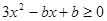 在[-2,1]上恒成立,
在[-2,1]上恒成立,
①
在x= 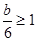 时,
时,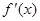 =
=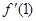 =3-b+b>0,∴
=3-b+b>0,∴
②在x= 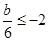 时,
时,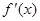 =
=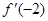 =12-2b+b>0,∴
=12-2b+b>0,∴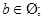
③在-2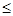
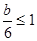 时,
时,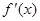 =
=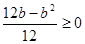 ,∴
,∴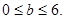
综合上述讨论可知,所求参数b的取值范围是b≥0. ………………12分
【解析】略

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 )
)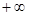 )
)