题目内容
本小题满分12分)
已知 函数f (x)=
函数f (x)= x3+ ax2-bx (a, b∈R) .
x3+ ax2-bx (a, b∈R) .
(1)若y=f (x)图象上的点(1,- )处的切线斜率为-4
)处的切线斜率为-4 ,求y=f (x)的极大值;
,求y=f (x)的极大值;
(2)若y=f (x)在区间[-1,2]上是单调减函数,求a + b的最小值.
解:(1)∵f ′(x)=x2+2ax-b ,
∴ 由题意可 知:f ′(1)=-4且f (1)=-
知:f ′(1)=-4且f (1)=- ,
,
∴ 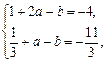 解得:
解得: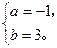 …………………………2分
…………………………2分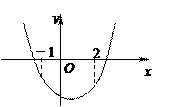
∴ f (x)= x3-x2-3x。
x3-x2-3x。
f ′(x)=x2-2x-3=(x+1)(x-3).
令f ′(x)= 0,得x1=-1,x2=3,……………3分
0,得x1=-1,x2=3,……………3分
由此可知:
∴ 当x=-1时, f (x)取极大值x (-∞,-1) -1 (-1, 3) 3 (3, +∞) f ’(x) + 0 - 0 + f (x) ↗ f (x)极大5/3 ↘ f (x) 极小 ↗ 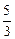 . …………………………6分
. …………………………6分
(2) ∵y=f (x)在区间[-1,2]上是单调减函数,
∴f ′(x)=x2+2ax-b≤0在区间[-1,2]上恒成立.
根据二次函数图象可知f ′(-1)≤0且f ′(2)≤0,即: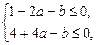 也即
也即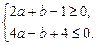 …………………9分
…………………9分
作出不等式组表示的平面区域如图:
当直线z=a +b经过交点P(-
+b经过交点P(-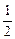 , 2)时,
, 2)时,
z=a+b取得最小值z=-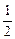 +2=
+2=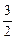 ,
,
∴z=a+b取得最小值为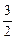 ……………………12分
……………………12分
解析

练习册系列答案
相关题目
 ,记函数
,记函数 ,
, 的最小正周期为
的最小正周期为 .
.  的值;
的值; 时,试求
时,试求 上的单调递增区间.
上的单调递增区间.
 是椭圆上纵坐标不为零的两点,若
是椭圆上纵坐标不为零的两点,若 其中F为椭圆的左焦点.
其中F为椭圆的左焦点. 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
 (
( )两点,且
)两点,且 .
. 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若 ,求
,求 的值.
的值. ,
, ,
, ,求实数
,求实数 的值;
的值; ,求实数
,求实数 ,且对于任意实数
,且对于任意实数 ,恒有
,恒有 .
. 的解析式;
的解析式;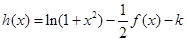 有几个零点?
有几个零点?