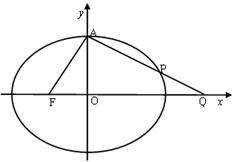
摘要： 设过椭圆焦点F作直线与椭圆相交 P.Q两点.A为椭圆长轴上一个顶点.连结AP 和AQ分别交相应于焦点F的椭圆准线于M.N两点.则MF⊥NF.
网址：http://m.1010jiajiao.com/timu3_id_522800[举报]
设椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| 8 |
| 5 |
| PQ |
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l：x+
| 3 |
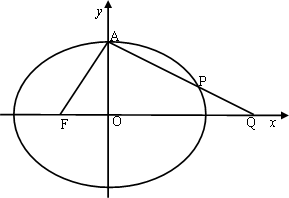
设椭圆C：
的左焦点为F，上顶点为A，过点A作垂直于AF的直线交椭圆C于另外一点P，交x轴正半轴于点Q， 且
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l： 
相切，求椭圆C的方程.
设椭圆
=1(a＞b＞0)的焦点分别为F1(-1,0)、F2(1,0),右准线l交x轴于点A,且
.
=1(a＞b＞0)的焦点分别为F1(-1,0)、F2(1,0),右准线l交x轴于点A,且.
(1)试求椭圆的方程;
(2)过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形DMEN面积的最大值和最小值.
(文)已知函数f(x)=
x3+bx2+cx,b、c∈R,且函数f(x)在区间(-1,1)上单调递增,在区间(1,3)上单调递减.
(1)若b=-2,求c的值;
(2)求证:c≥3;
(3)设函数g(x)=f′(x),当x∈［-1,3］时,g(x)的最小值是-1,求b、c的值.
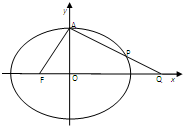
查看习题详情和答案>>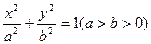
的左焦点为F，上顶点为A，过点A作垂直于AF的直线交椭圆C于另外一点P，交x轴正半轴于点Q，且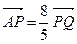
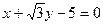相切，求椭圆C的方程. 
的左焦点为F，上顶点为A，过点A作垂直于AF的直线交椭圆C于另外一点P，交x轴正半轴于点Q，且
y－5＝0相切，求椭圆C的方程．