Question

设椭圆C：的左焦点为F，上顶点为A，过点A作垂直于AF的直线交椭圆C于另外一点P，交x轴正半轴于点Q， 且

   （1）求椭圆C的离心率；

   （2）若过A、Q、F三点的圆恰好与直线l： 相切，求椭圆C的方程.

Answer 1

（1）

（2）

解析:

⑴设Q（x₀，0），由F（-c，0）

A（0，b）知

…2分

设，得………4分

因为点P在椭圆上，所以………6分

整理得2b²=3ac，即2（a²－c²）=3ac，,故椭圆的离心率e＝………8分

⑵由⑴知，

于是F（－a，0）， Q

△AQF的外接圆圆心为（a，0），半径r=|FQ|=a…………10分

所以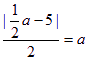，解得a=2，∴c=1，b=，

所求椭圆方程为