摘要： 椭圆G:的两个焦点F1.F2(c.0).M是椭圆上的一点.且满足 (Ⅰ)求离心率e的取值范围, (Ⅱ)当离心率e取得最小值时.点N(0.3)到椭圆上的点的最远距离为 (1)求此时椭圆G的方程, 的直线l与椭圆G相交于不同的两点A. B.Q为AB的中点.问A.B两点能否关于过点的直线对称?若能.求出k
网址：http://m.1010jiajiao.com/timu3_id_520968[举报]
椭圆G：
的两个焦点F1（－c，0）、F2（c，0），M是椭圆上的一点，且满足
（Ⅰ）求离心率e的取值范围；
（Ⅱ）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为
求此时椭圆G的方程；（ⅱ）设斜率为k（k≠0）的直线l与椭圆G相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点
的直线对称？若能，求出k的取值范围；若不能，请说明理由
椭圆G：
的两个焦点为F1、F2，短轴两端点B1、B2，已知F1、F2、B1、B2四点共圆 ，且点N（0，3）到椭圆上的点的最远距离为
（1）求此时椭圆G的方程；
（2）设斜率为k（k≠0）的直线m与椭圆G相交于不同的两点E、F，Q为EF的中点，问E、F两点能否关于过点
的直线对称？若能，求出k的取值范围；若不能，请说明理由。
(本题满分14分)
椭圆G：
的两个焦点为F1、F2，短轴两端点B1、B2，已知
F1、F2、B1、B2四点共圆，且点N（0，3）到椭圆上的点最远距离为
（1）求此时椭圆G的方程；
（2）设斜率为k（k≠0）的直线m与椭圆G相交于不同的两点E、F，Q为EF的中点，问E、F两点能否关于过点P（0，
）、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．
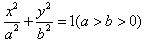的两个焦点为F1、F2，点P在椭圆G上，且PF1⊥F1F2，且
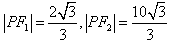，斜率为1的直线l与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3，2），
的两个焦点为F1、F2，短轴两端点B1、B2，已知F1、F2、B1、B2四点共圆，且点N(0，3)到椭圆上的点最远距离为
)、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．