题目内容
椭圆G：
的两个焦点为F1、F2，短轴两端点B1、B2，已知F1、F2、B1、B2四点共圆，且点N(0，3)到椭圆上的点最远距离为
(1)求此时椭圆G的方程；
(2)设斜率为k(k≠0)的直线m与椭圆G相交于不同的两点E、F，Q为EF的中点，问E、F两点能否关于过点P(0，
)、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．
答案：
解析：
解析：
|
解：(1)根据椭圆的几何性质，线段F1F2与线段B1B2互相垂直平分，故椭圆中心即为该四点外接圆的圆心 1分 故该椭圆中 设H(x，y)为椭圆上一点，则 若 由 若 由 (1)设 两式相减得 又直线PQ⊥直线m ∴直线PQ方程为 将点Q( 由③④得Q( 而Q点必在椭圆内部 由此得 时，E、F两点关于点P、Q的直线对称 14分 |
即椭圆方程可为
3分
4分
，则
有最大值
5分
(舍去)(或b2＋3b＋9＜27，故无解) 6分
7分
∴所求椭圆方程为
8分
，则由
③
)代入上式得，
④ 11分
) 12分
，
，故当
练习册系列答案
相关题目
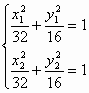
的两个焦点为
是椭圆上一点，且满
．[来源:学#科#网]
的取值范围；
到椭圆上点的最远距离为
．
的直线
与椭圆G相交于不同两点
，
为
的中点，问：
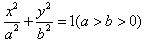的两个焦点为F1、F2，点P在椭圆G上，且PF1⊥F1F2，且
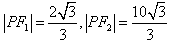，斜率为1的直线l与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3，2），
的两个焦点为F1、F2，短轴两端点B1、B2，已知F1、F2、B1、B2四点共圆 ，且点N（0，3）到椭圆上的点的最远距离为
的直线对称？若能，求出k的取值范围；若不能，请说明理由。
的两个焦点为F1、F2，短轴两端点B1、B2，已知
）、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．
的两个焦点为
是椭圆上一点，且满
．
的取值范围；
到椭圆上点的最远距离为
．
的直线
与椭圆G相交于不同两点
，
为
的中点，问：