摘要：19．解:(1)在直三棱柱ABC-A1B1C1中. (1)∵. ∴为异面直线AD与A1B1所成的角. ---------2分.连结BD. 在中.∵AC=4. ∴. 在中.∵BC=3.CD=2.∴. 在△ABD中.∵AB=5. ∴异面直线AD与A1B1所成角的余弦值为------------4分 (2)证明:∵AB=5.BC=3.AC=4.∴. ∵底面ABC⊥侧面ACC1A1.∴BC⊥侧面ACC1A1.------------6分 取AB.AC的中点E.F.连结EF.A1F.则EF//BC. ∴EF⊥平面ACC1A1. ∴A1F为A1E在侧面AC1内的射影. 在正方形C1CAA1内.∵ D.F分别为CC1.AC的中点. ∴≌.∴. ∴.∴. ∴------8分 (3)连结.过D作DH⊥.垂足为H. ∵EF//BC.BC//B1C1.∴EF// B1C1.∴点F在平面B1C1E内. ∵EF⊥平面ACC1A1.平面ACC1A1.EF⊥DH.------10分 ∵..∴DH⊥平面B1C1E. 在中.∵.∴.-----12分
网址：http://m.1010jiajiao.com/timu3_id_520047[举报]
（2012•泸州一模）如图，在直三棱柱ABC-A′B′C′中，AB=BC=CA=a，
如图，在直三棱柱ABC-A′B′C′中，点D是BC的中点，∠ACB=90°，AC=BC=1，AA′=2，（1）欲过点A′作一截面与平面AC'D平行，问应当怎样画线，写出作法，并说明理由；
（2）求异面直线BA′与 C′D所成角的余弦值．
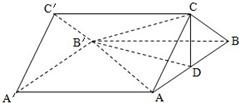如图，在直三棱柱ABC-A′B′C′中，已知AA′=4，AC=BC=2，∠ACB=90°，D是AB的中点．（Ⅰ）求证：CD⊥AB′；
（Ⅱ）求二面角A′-AB′-C的大小；
（Ⅲ）求直线B′D与平面AB′C所成角的正弦值． 查看习题详情和答案>>
如图，在直三棱柱ABC-A′B′C′中，AA′=AB=BC=1，∠ABC=90°．棱A′C′上有两个动点E，F，且EF=a （a为常数）．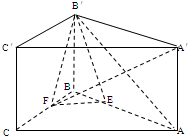
如图，在直三棱柱ABC-A′B′C′中，AB=BC=BB′=a，∠ABC=90°，点E、F分别是棱AB、BC上的动点，且AE=BF．