题目内容
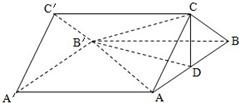 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.(Ⅰ)求证:CD⊥AB′;
(Ⅱ)求二面角A′-AB′-C的大小;
(Ⅲ)求直线B′D与平面AB′C所成角的正弦值.
分析:(Ⅰ)欲证CD⊥AB′,可先证CD⊥平面ABB′A′,欲证CD⊥平面ABB′A′,可根据平面ABC与平面ABB′A′垂直的性质定理可得;
(Ⅱ)过D作DE⊥AB′,垂足为E,连接CE.由三垂线定理可知CE⊥AB′,根据二面角的平面角的定义可知∠CED是二面角B-AB′-C的平面角,在三角形CED中求出此角,而根据二面角A′-AB′-C与二面角B-AB'-C的大小互补即可求出二面角A′-AB′-C的大小;
(Ⅲ)过D作DF⊥CE,垂足为F,连接B′F,根据线面所成角的定义可知∠DB′F为直线B'D与平面AB'C所成的角,在直角三角形DB′F中求出此角的正弦值即可.
(Ⅱ)过D作DE⊥AB′,垂足为E,连接CE.由三垂线定理可知CE⊥AB′,根据二面角的平面角的定义可知∠CED是二面角B-AB′-C的平面角,在三角形CED中求出此角,而根据二面角A′-AB′-C与二面角B-AB'-C的大小互补即可求出二面角A′-AB′-C的大小;
(Ⅲ)过D作DF⊥CE,垂足为F,连接B′F,根据线面所成角的定义可知∠DB′F为直线B'D与平面AB'C所成的角,在直角三角形DB′F中求出此角的正弦值即可.
解答:解:(Ⅰ)证明:因为AC=BC,D是AB的中点,所以CD⊥AB.
由已知,三棱柱ABC-A′B′C′是直三棱柱,
所以平面ABC⊥平面ABB′A′.
所以CD⊥平面ABB′A′.
又因为AB′?平面ABB′A′,
所以CD⊥AB′.(5分)
(Ⅱ)解:由(Ⅰ)知CD⊥平面ABB′A′.
过D作DE⊥AB′,垂足为E,连接CE.
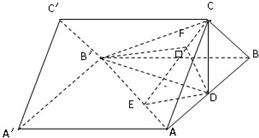 由三垂线定理可知CE⊥AB′,
由三垂线定理可知CE⊥AB′,
所以∠CED是二面角B-AB′-C的平面角.
由已知可求得CD=
,DE=
,
所以tan∠CED=
=
.
所以二面角B-AB′-C的大小为arctan
.
由于二面角A′-AB′-C与二面角B-AB'-C的大小互补,
所以二面角A′-AB′-C的大小为π-arctan
.(10分)
(Ⅲ)过D作DF⊥CE,垂足为F,连接B′F.
由(Ⅱ)可证得AB′⊥平面CDE,所以AB′⊥DF,可证得DF⊥平面AB'C.
所以,∠DB′F为直线B'D与平面AB'C所成的角.
在直角三角形CDE中,可知CE=
,所以DF=
=
.
在直角三角形BB′D中,可知B′D=3
.
在直角三角形DB′F中,sin∠DB′F=
=
.
所以直线B'D与平面AB'C所成角的正弦值为
.(14分)
由已知,三棱柱ABC-A′B′C′是直三棱柱,
所以平面ABC⊥平面ABB′A′.
所以CD⊥平面ABB′A′.
又因为AB′?平面ABB′A′,
所以CD⊥AB′.(5分)
(Ⅱ)解:由(Ⅰ)知CD⊥平面ABB′A′.
过D作DE⊥AB′,垂足为E,连接CE.
 由三垂线定理可知CE⊥AB′,
由三垂线定理可知CE⊥AB′,所以∠CED是二面角B-AB′-C的平面角.
由已知可求得CD=
| 2 |
| 2 | ||
|
所以tan∠CED=
| CD |
| DE |
| ||
| 2 |
所以二面角B-AB′-C的大小为arctan
| ||
| 2 |
由于二面角A′-AB′-C与二面角B-AB'-C的大小互补,
所以二面角A′-AB′-C的大小为π-arctan
| ||
| 2 |
(Ⅲ)过D作DF⊥CE,垂足为F,连接B′F.
由(Ⅱ)可证得AB′⊥平面CDE,所以AB′⊥DF,可证得DF⊥平面AB'C.
所以,∠DB′F为直线B'D与平面AB'C所成的角.
在直角三角形CDE中,可知CE=
| ||
| 3 |
| CD•DE |
| CE |
2
| ||
| 5 |
在直角三角形BB′D中,可知B′D=3
| 2 |
在直角三角形DB′F中,sin∠DB′F=
| DF |
| DB′ |
| ||
| 15 |
所以直线B'D与平面AB'C所成角的正弦值为
| ||
| 15 |
点评:本题主要考查了空间两直线的位置关系,以及二面角及其度量和直线与平面的位置关系,考查空间想象能力,几何逻辑推理能力,以及计算能力.

练习册系列答案
相关题目




