Question

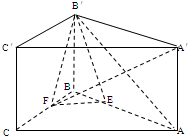如图，在直三棱柱ABC-A′B′C′中，AB=BC=BB′=a，∠ABC=90°，点E、F分别是棱AB、BC上的动点，且AE=BF．
（I）求证：A′F⊥AB′．
（II）当三棱锥B′-BEF的体积取得最大值时，求二面角B-B′F-E的余弦值．

Answer 1

分析：（I）连接AB′，A′B，利用线面垂直的判定证明AB′⊥面A′FB，即可证得A′F⊥AB′；
（II）求得三棱锥B′-BEF的体积取得最大值时，E、F分别为AB与BC的中点，建立空间直角坐标系，求出平面的法向量，利用向量的夹角公式，即可求出二面角B-B′F-E的余弦值．

解答：（I）证明：连接AB′，A′B
由题设知侧面ABB′A′为正方形，∴AB′⊥A′B，
又CB⊥AB，CB⊥BB′，AB∩BB′=B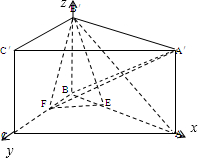
∴CB⊥侧面ABB′A′，∴CB⊥AB′∴FB⊥AB′
∵A′B∩FB=B
∴AB′⊥面A′FB
∵A′F?面A′FB
∴A′F⊥AB′
（II）设AE=x，则BE=a-x
∴三棱锥B′-BEF的体积为

1

6

a(a-x)x≤

a3

24

，当且仅当x=

a

2

时取等号，此时E、F分别为AB与BC的中点． 
以B为原点，BA为x轴，BC为y轴，BB′为z轴建立空间直角坐标系，则B（0，0，0），A（a，0，0），C（0，a，0），B′（0，0，a），E（

a

2

，0，0），F（0，

a

2

，0）

BA

为平面BB′F的一个法向量，且

BA

=（a，0，0），
设平面EB′F的法向量为

n

=(x，y，z)
由

n • B′E =0 n • EF =0

得

ax 2 -az=0 - ax 2 + ay 2 =0

取z=1，则

n

=(2，1，1)
∴cosθ=

n • BA

| n || BA |

=

2a

6 a

=

6

3

．

点评：本题以直三棱柱为载体主要考查空间中的线线、线面、面面之间的平行与垂直关系，第二问主要考查简单的二面角的计算，属于中档题．