题目内容
 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
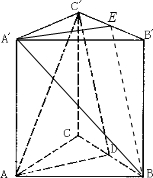
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,(1)欲过点A′作一截面与平面AC'D平行,问应当怎样画线,写出作法,并说明理由;
(2)求异面直线BA′与 C′D所成角的余弦值.
分析:(1)取B′C′的中点E,连接A′E,BE,A′B,根据面面平行的判定定理证明平面AC′D∥平面A′BE;
(2)证明∠A′BE为异面直线BA′与 C′D所成角,解△A′BE,利用余弦定理求得∠A′BE的余弦值.
(2)证明∠A′BE为异面直线BA′与 C′D所成角,解△A′BE,利用余弦定理求得∠A′BE的余弦值.
解答:解:(1)取B′C′的中点E,连接A′E,BE,A′B,
∵截面与平面AC'D平行,∴截面与平面BCC′B′的交线BE∥BC′,∵D是BC的中点,∴E是B′C′的中点;
∵A′E∥AD,∴A′E∥平面AC′D,又A′E∩BE=E,∴平面AC′D∥平面A′BE.
(2)∵BE∥DC′,∴∠A′BE为异面直线BA′与 C′D所成角,
∵∠ACB=90°,
∴在△A′BE中,BE=
,A′B=
,A′E=
,
∴cos∠A′BE=
=
.
∵截面与平面AC'D平行,∴截面与平面BCC′B′的交线BE∥BC′,∵D是BC的中点,∴E是B′C′的中点;
∵A′E∥AD,∴A′E∥平面AC′D,又A′E∩BE=E,∴平面AC′D∥平面A′BE.
(2)∵BE∥DC′,∴∠A′BE为异面直线BA′与 C′D所成角,
∵∠ACB=90°,
∴在△A′BE中,BE=
| ||
| 2 |
| 6 |
| ||
| 2 |
∴cos∠A′BE=
| BE2+A′B2-A′E2 |
| 2×BE×A′B |
3
| ||
| 34 |

点评:本题考查了面面平行的性质与判定,考查了异面直线所成的角及求法,考查了学生的空间想象能力与运算能力,解题的关键是熟练掌握面面平行的判定定理与性质定理.

练习册系列答案
相关题目




