摘要:22. 如图.设抛物线的焦点为F.动点P在直线上运动.过P作抛物线C的两条切线PA.PB.且与抛物线C分别相切于A.B两点. (1)求△APB的重心G的轨迹方程. (2)证明∠PFA=∠PFB.
网址:http://m.1010jiajiao.com/timu3_id_518166[举报]
(本小题满分14分)
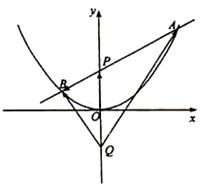
如图,过抛物线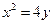 的对称轴上任一点
的对称轴上任一点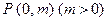 作直线与抛物线交于
作直线与抛物线交于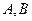 两点,点
两点,点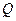 是点
是点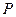 关于原点的对称点.
关于原点的对称点.
(1) 设点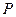 分有向线段
分有向线段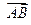 所成的比为
所成的比为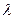 ,证明:
,证明:
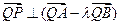 ;
;
(2) 设直线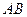 的方程是
的方程是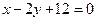 ,过
,过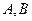 两点的圆
两点的圆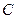 与抛物线在点
与抛物线在点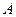 处有共同的切线,求圆
处有共同的切线,求圆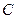 的方程.
的方程.
如图,过抛物线
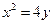 的对称轴上任一点
的对称轴上任一点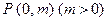 作直线与抛物线交于
作直线与抛物线交于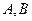 两点,点
两点,点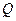 是点
是点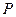 关于原点的对称点.
关于原点的对称点.
(1) 设点
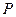 分有向线段
分有向线段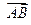 所成的比为
所成的比为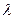 ,证明:
,证明:
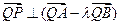 ;
;(2) 设直线
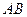 的方程是
的方程是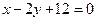 ,过
,过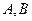 两点的圆
两点的圆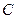 与抛物线在点
与抛物线在点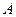 处有共同的切线,求圆
处有共同的切线,求圆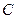 的方程.
的方程.(本小题满分14分)
设![]() 椭圆方程为
椭圆方程为![]() 抛物线方程为
抛物线方程为![]() 如图4所示,过点
如图4所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点![]()
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。

(本小题满分14分)
设 椭圆方程为
椭圆方程为 抛物线方程为
抛物线方程为 如图4所示,过点
如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。

查看习题详情和答案>>
 椭圆方程为
椭圆方程为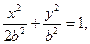 抛物线方程为
抛物线方程为 如图4所示,过点
如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
