Question

（08年山东卷理）(本小题满分14分)

如图，设抛物线方程为x²=2py(p＞0),M为 直线y=-2p上任意一点，过M引抛物线的切线，切点分别为A，B.

（Ⅰ）求证：A，M，B三点的横坐标成等差数列；

（Ⅱ）已知当M点的坐标为（2，-2p）时，，求此时抛物线的方程；

（Ⅲ）是否存在点M，使得点C关于直线AB的对称点D在抛物线上，其中，点C满足（O为坐标原点）.若存在，求出所有适合题意的点M的坐标；若不存在，请说明理由.

 

Answer 1

【解析】（Ⅰ）证明：由题意设

                     由得，则

                     所以

                     因此直线MA的方程为

　　　　　　　　直线MB的方程为

                     所以                   ①

                   ②

由①、②得

因此，即

所以A、M、B三点的横坐标成等差数列.

（Ⅱ）解：由（Ⅰ）知，当x₀=2时，

                将其代入①、②并整理得：

              　

              　

　　　　　所以　x₁、x₂是方程的两根，

              因此

              又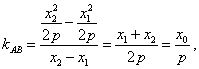

              所以

              由弦长公式得

             

　　　　又，

              所以p=1或p=2，

              因此所求抛物线方程为或

（Ⅲ）解：设D(x₃,y₃)，由题意得C(x₁+ x₂, y₁+ y₂),

                则CD的中点坐标为

              　设直线AB的方程为

              　由点Q在直线AB上，并注意到点也在直线AB上，

              　代入得

              　若D（x₃,y₃）在抛物线上，则

              　因此　x₃=0或x₃=2x₀.

                即D(0，0)或

              （1）当x₀=0时，则，此时，点M(0,-2p)适合题意.

              （2）当，对于D(0，0)，此时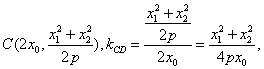

              　　又AB⊥CD，

所以

即矛盾.

对于因为此时直线CD平行于y轴，

又

所以直线AB与直线CD不垂直，与题设矛盾，

所以时，不存在符合题意的M点.

综上所述，仅存在一点M(0，-2p)适合题意.