摘要：已知之间满足 .动点(x,y)在曲线(b>0)上变化.求x2+2y的最大值,
网址：http://m.1010jiajiao.com/timu3_id_517642[举报]
已知x、y之间满足
+
=1(b＞0)
（1）方程
+
=1(b＞0)表示的曲线经过一点(
，
)，求b的值
（2）（理做文不做）动点（x，y）在曲线
+
=1（b＞0）上变化，求x2+2y的最大值．
查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| b2 |
（1）方程
| x2 |
| 4 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
（2）（理做文不做）动点（x，y）在曲线
| x2 |
| 4 |
| y2 |
| b2 |
已知x、y之间满足
+
=1(b＞0)
（1）方程
+
=1(b＞0)表示的曲线经过一点(
，
)，求b的值
（2）动点（x，y）在曲线
+
=1（b＞0）上变化，求x2+2y的最大值；
（3）由
+
=1(b＞0)能否确定一个函数关系式y=f（x），如能，求解析式；如不能，再加什么条件就可使x、y之间建立函数关系，并求出解析式．
查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| b2 |
（1）方程
| x2 |
| 4 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
（2）动点（x，y）在曲线
| x2 |
| 4 |
| y2 |
| b2 |
（3）由
| x2 |
| 4 |
| y2 |
| b2 |
已知x、y之间满足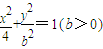
（1）方程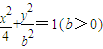
表示的曲线经过一点
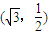，求b的值
（2）动点（x，y）在曲线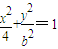
（b＞0）上变化，求x2+2y的最大值；
（3）由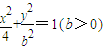
能否确定一个函数关系式y=f（x），如能，求解析式；如不能，再加什么条件就可使x、y之间建立函数关系，并求出解析式．
查看习题详情和答案>>
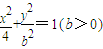
（1）方程
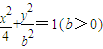表示的曲线经过一点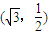，求b的值（2）动点（x，y）在曲线
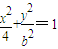（b＞0）上变化，求x2+2y的最大值；（3）由
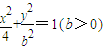能否确定一个函数关系式y=f（x），如能，求解析式；如不能，再加什么条件就可使x、y之间建立函数关系，并求出解析式．查看习题详情和答案>>
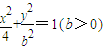
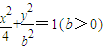表示的曲线经过一点
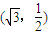，求b的值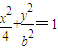
（b＞0）上变化，求x2+2y的最大值；
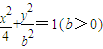能否确定一个函数关系式y=f（x），如能，求解析式；如不能，再加什么条件就可使x、y之间建立函数关系，并求出解析式．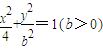
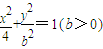表示的曲线经过一点
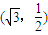，求b的值
（b＞0）上变化，求x2+2y的最大值．