题目内容
已知x、y之间满足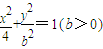
(1)方程
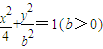 表示的曲线经过一点
表示的曲线经过一点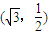 ,求b的值
,求b的值(2)动点(x,y)在曲线
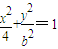 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;(3)由
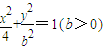 能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
【答案】分析:(1)根据题意把点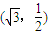 代入曲线的方程
代入曲线的方程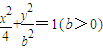 可得答案.
可得答案.
(2)由题意可得: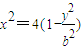 ,所以
,所以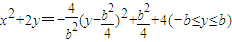 ,再利用二次函数的有关性质求出其最大值.
,再利用二次函数的有关性质求出其最大值.
(3)根据函数的定义可得曲线的方程不能表示函数,并且结合函数的定义若x、y满足xy<0时,x、y之间能够建立函数关系,并且根据方程也可以得到函数解析式.
解答:解:(1)由题意可得:曲线经过一点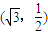 ,
,
所以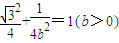 ,
,
解得:b=1.(4分)
(2)根据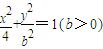 得
得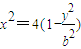 (5分)
(5分)
所以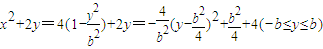 (7分)
(7分)
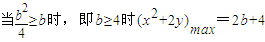 ,
,
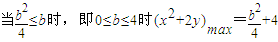
∴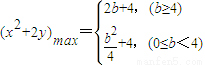 (10分)
(10分)
(2)不能; (11分)
如再加条件xy<0就可使x、y之间建立函数关系,(12分)
并且解析式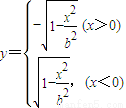 .(14分)
.(14分)
点评:本题主要考查椭圆的标准方程与二次函数的性质,以及函数的有关定义,此题属于中档题.
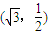 代入曲线的方程
代入曲线的方程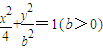 可得答案.
可得答案.(2)由题意可得:
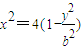 ,所以
,所以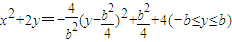 ,再利用二次函数的有关性质求出其最大值.
,再利用二次函数的有关性质求出其最大值.(3)根据函数的定义可得曲线的方程不能表示函数,并且结合函数的定义若x、y满足xy<0时,x、y之间能够建立函数关系,并且根据方程也可以得到函数解析式.
解答:解:(1)由题意可得:曲线经过一点
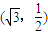 ,
,所以
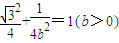 ,
,解得:b=1.(4分)
(2)根据
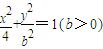 得
得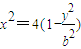 (5分)
(5分)所以
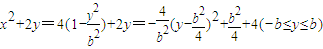 (7分)
(7分)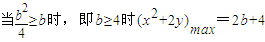 ,
,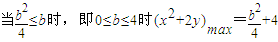
∴
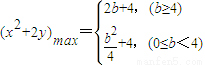 (10分)
(10分)(2)不能; (11分)
如再加条件xy<0就可使x、y之间建立函数关系,(12分)
并且解析式
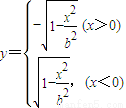 .(14分)
.(14分)点评:本题主要考查椭圆的标准方程与二次函数的性质,以及函数的有关定义,此题属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
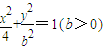
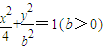 表示的曲线经过一点
表示的曲线经过一点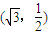 ,求b的值
,求b的值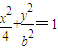 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;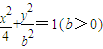 能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.