题目内容
已知x、y之间满足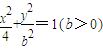
(1)方程
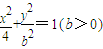 表示的曲线经过一点
表示的曲线经过一点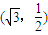 ,求b的值
,求b的值(2)(理做文不做)动点(x,y)在曲线
 (b>0)上变化,求x2+2y的最大值.
(b>0)上变化,求x2+2y的最大值.
【答案】分析:(1)把已知点代入椭圆的方程求得b.
(2)利用椭圆的方程可表示出x2,进而把x2+2y整理成关于y的函数解析式,分别看当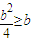 和
和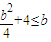 时x2+2y的最大值.
时x2+2y的最大值.
解答:解:(1)把点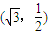 代入
代入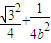 =1(b>0)∴b=1
=1(b>0)∴b=1
(2)根据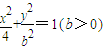 得
得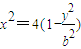
∴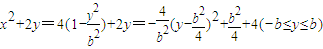
当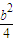 ≥b时,即b≥4时(x2+2y)max=2b+4当
≥b时,即b≥4时(x2+2y)max=2b+4当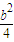 ≤b时,即0≤b≤4时(x2+2y)max=
≤b时,即0≤b≤4时(x2+2y)max=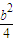 +4
+4
∴(x2+2y)max=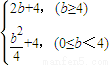
点评:本题主要考查了曲线与方程的问题.考查了学生分析问题和解决问题的能力.
(2)利用椭圆的方程可表示出x2,进而把x2+2y整理成关于y的函数解析式,分别看当
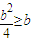 和
和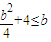 时x2+2y的最大值.
时x2+2y的最大值.解答:解:(1)把点
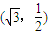 代入
代入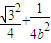 =1(b>0)∴b=1
=1(b>0)∴b=1(2)根据
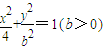 得
得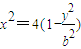
∴
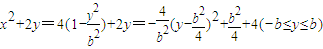
当
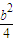 ≥b时,即b≥4时(x2+2y)max=2b+4当
≥b时,即b≥4时(x2+2y)max=2b+4当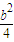 ≤b时,即0≤b≤4时(x2+2y)max=
≤b时,即0≤b≤4时(x2+2y)max=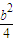 +4
+4∴(x2+2y)max=
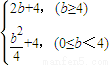
点评:本题主要考查了曲线与方程的问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
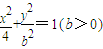
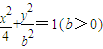 表示的曲线经过一点
表示的曲线经过一点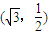 ,求b的值
,求b的值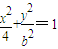 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;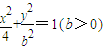 能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.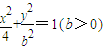
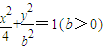 表示的曲线经过一点
表示的曲线经过一点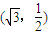 ,求b的值
,求b的值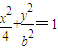 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;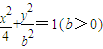 能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.