摘要:平面直角坐标系中.O为坐标原点.给定两点A.点C满足 . (1)求点C的轨迹方程, (2)设点C的轨迹与椭圆交于两点M.N.且以MN为直径的圆过原点.求证: 的条件下.若椭圆的离心率不大于.求椭圆实轴长的取值范围. 解:(1)设 即点C的轨迹方程为x+y=1 . (2) 得:(a2+b2)x2-2a2x+ a2- a2b2=0 设M(x1,y1),N(x2,y2).则“ x1+ x2=. x1x2= 因为以MN为直径的圆过原点为. 所以=0.即x1x2+y1y2=0 ∴x1x2+(1-x1)(1-x2)=1-(x1+ x2)+2 x1x2=1-+2=0 即a2+b2-2 a2b2=0 ∴ (3) ∴椭圆实轴长的取值范围是(0,.
网址:http://m.1010jiajiao.com/timu3_id_516864[举报]
平面直角坐标系中,O为坐标原点,设向量
=
,
=
,其中
=(3,1),
=(1,3),若
=λ
+μ
,且0≤μ≤λ≤1,那么C点所有可能的位置区域用阴影表示正确的是( )
| OA |
| a |
| OB |
| b |
| a |
| b |
| OC |
| a |
| b |
A、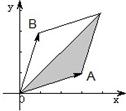 |
B、 |
C、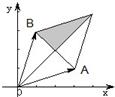 |
D、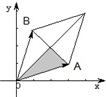 |
平面直角坐标系中,O为坐标原点,已知两点A(3,1)、B(-1,3),若点C满足
=α
+β
,其中α、β∈R,且α+β=1,则点C的轨迹方程为( )
| OC |
| OA |
| OB |
| A、3x+2y-11=0 |
| B、(x-1)2+(y-2)2=5 |
| C、2x-y=0 |
| D、x+2y-5=0 |