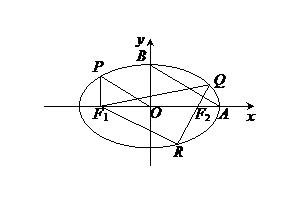
摘要:21.如图.分别为椭圆和双曲线的右焦点.A.B为椭圆和双曲线的公共顶点.P.Q分别为双曲线和椭圆上不同于A.B的第一象限内的点.且满足 =,. ⑴求出椭圆和双曲线的离心率, (2)设直线PA.PB.QA.QB的斜率分别是 ,.求证:.
网址:http://m.1010jiajiao.com/timu3_id_514760[举报]
(本题满分12分)如图,已知椭圆 焦点为
焦点为 ,双曲线
,双曲线 ,设
,设 是双曲线
是双曲线 上异于顶点的任一点,直线
上异于顶点的任一点,直线 与椭圆的交点分别为
与椭圆的交点分别为 和
和 。
。
(1) 设直线 的斜率分别为
的斜率分别为 和
和 ,求
,求 的值;
的值;
(2) 是否存在常数 ,使得
,使得 恒成立?若存在,试求出
恒成立?若存在,试求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。

查看习题详情和答案>>
(本小题满分12分)如图,已知![]() 分别为椭圆
分别为椭圆![]() 的下顶点和上顶点,
的下顶点和上顶点,![]() 为椭圆的下焦点,
为椭圆的下焦点,![]() 为椭圆上异于
为椭圆上异于![]() 点的任意一点,直线
点的任意一点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 点
点
(1)当点![]() 位于
位于![]() 轴右侧,且
轴右侧,且![]() ∥
∥![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)是否存在![]() 值,使得以
值,使得以![]() 为直径的圆过
为直径的圆过![]() 点?若存在加以证明,若不存在,请说明理由;
点?若存在加以证明,若不存在,请说明理由;
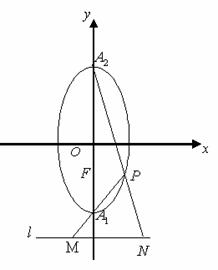 (3)由(2)问所得
(3)由(2)问所得![]() 值,求线段
值,求线段![]() 最小值.
最小值.
(本小题满分12分)如图,已知![]() 分别为椭圆
分别为椭圆![]() 的下顶点和上顶点,
的下顶点和上顶点,![]() 为椭圆的下焦点,
为椭圆的下焦点,![]() 为椭圆上异于
为椭圆上异于![]() 点的任意一点,直线
点的任意一点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 点
点
(1)当点![]() 位于
位于![]() 轴右侧,且
轴右侧,且![]() ∥
∥![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)是否存在![]() 值,使得以
值,使得以![]() 为直径的圆过
为直径的圆过![]() 点?若存在加以证明,若不存在,请说明理由;
点?若存在加以证明,若不存在,请说明理由;
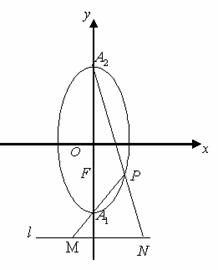 (3)由(2)问所得
(3)由(2)问所得![]() 值,求线段
值,求线段![]() 最小值.
最小值.
 (2)过右焦点
(2)过右焦点 是以原点O为中心、
是以原点O为中心、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线 为钝角,若
为钝角,若 ,
, .
. 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.