题目内容
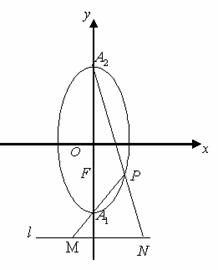
(本小题满分12分)如图,已知![]() 分别为椭圆
分别为椭圆![]() 的下顶点和上顶点,
的下顶点和上顶点,![]() 为椭圆的下焦点,
为椭圆的下焦点,![]() 为椭圆上异于
为椭圆上异于![]() 点的任意一点,直线
点的任意一点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 点
点
(1)当点![]() 位于
位于![]() 轴右侧,且
轴右侧,且![]() ∥
∥![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)是否存在![]() 值,使得以
值,使得以![]() 为直径的圆过
为直径的圆过![]() 点?若存在加以证明,若不存在,请说明理由;
点?若存在加以证明,若不存在,请说明理由;
 (3)由(2)问所得
(3)由(2)问所得![]() 值,求线段
值,求线段![]() 最小值.
最小值.
(1)![]() 时,
时,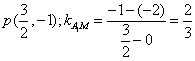
直线![]() 方程
方程![]() ------------3分
------------3分
(2)![]()
![]()
若以![]() 为直径的圆过点
为直径的圆过点![]() ,则
,则![]() ,得
,得![]() ------5分
------5分
![]() --------7分
--------7分
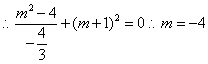 ---------9分
---------9分
(3)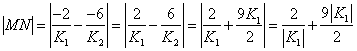
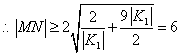 ,当且仅当
,当且仅当![]() 时,
时,![]() 最小值为6 --------12分
最小值为6 --------12分

练习册系列答案
相关题目