摘要：培养运用不等式研究函数.方程等问题及运用函数.方程等思想解决不等式问题的能力. 例题讲解 例题1 (1) 关于的不等式()的解为 A B C D (2) 设.则下列不等式不恒成立的是 A B C D (3) 设且则 ( ) A B C D (4)在R上定义运算若不等式对任意实数成立.则 A B C D (5) 已知,,则 . (6) 已知.则函数的最小值是 . 例题2 某村计划建造一个室内面积为800的矩形蔬菜温室.在温室内.沿左.右两侧后 侧内墙各保留1宽的通道.沿前侧内墙保留3宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少? 例题3 已知为实数, (1) 求导数; (2) 若,求在上的最大值和最小值; (3) 若在和上都是递增的,求的取值范围. 例题4 设 (1) 当时,恒成立,求的取值范围; (2) 当时, ,求的最小值. 例题5已知实数满足:关于的不等式对一切均成立. (1) 请验证满足题意, (2) 求出所有满足题意的实数.并说明理由, (3) 若对一切.均有不等式成立.求实数的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_511312[举报]
（2006•宝山区二模）给出函数f(x)=
+tx（x∈R）．
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
时，可以将f（x）化成f(x)=a(
+x)+b(
-x)的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
+h(x)，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
| x2+4 |
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
| 1 |
| 2 |
| x2+4 |
| x2+4 |
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
| g(x) |
给出函数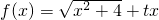
（x∈R）
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当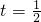
时，可以将f（x）化成
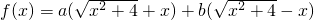的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记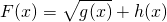
，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
已知
，函数
（其中
为自然对数的底数）．
（Ⅰ）求函数
在区间
上的最小值；
（Ⅱ）设数列
的通项
，
是前
项和，证明：
．
【解析】本试题主要考查导数在研究函数中的运用，求解函数给定区间的最值问题，以及能结合数列的相关知识，表示数列的前n项和，同时能构造函数证明不等式的数学思想。是一道很有挑战性的试题。
查看习题详情和答案>>
已知函数
（Ⅰ）若函数f（x）在[1，2]上是减函数，求实数a的取值范围；
（Ⅱ）令g（x）= f（x）－x2，是否存在实数a，当x∈（0，e](e是自然常数)时，函数g（x）的最小值是3，若存在，求出a的值；若不存在，说明理由；
（Ⅲ）当x∈（0，e]时，证明：
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f（x）在[1，2]上是减函数，的导函数恒小于等于零，然后分离参数求解得到a的取值范围。第二问中，
假设存在实数a，使
有最小值3，利用
，对a分类讨论，进行求解得到a的值。
第三问中，
因为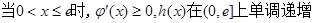
，这样利用单调性证明得到不等式成立。
解：(Ⅰ) 
(Ⅱ) 
（Ⅲ）见解析
查看习题详情和答案>>
的单调性；
的取值范围；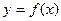
对于区间D上的任意两个值x1、x2总有以下不等式
成立，则称函数
，试判断函数