题目内容
已知 ,函数
,函数 (其中
(其中 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求函数 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)设数列 的通项
的通项 ,
, 是前
是前 项和,证明:
项和,证明: .
.
【解析】本试题主要考查导数在研究函数中的运用,求解函数给定区间的最值问题,以及能结合数列的相关知识,表示数列的前n项和,同时能构造函数证明不等式的数学思想。是一道很有挑战性的试题。
【答案】
解:(1) 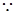
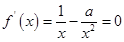
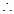
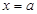
若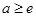 时, 函数
时, 函数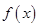 在区间
在区间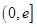 是减函数
是减函数 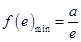 ;
;
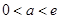 时 函数
时 函数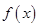 在区间
在区间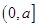 是减函数,
是减函数, 是增函数
是增函数
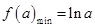 ;
;
综上所述 略
(2)由(1)可知,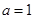 时,函数
时,函数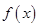 在定义域的最小值为0,
在定义域的最小值为0,
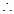
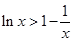 在
在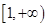 上成立
上成立
令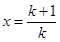 得
得 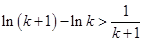
令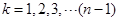
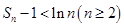
【解析】略

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
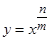 ,其中
,其中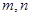 是取自集合
是取自集合 的两个不同值,则该函数为偶函数的概率为_____.
的两个不同值,则该函数为偶函数的概率为_____.