摘要:能够直接利用公式求等差和等比数列的通项;
网址:http://m.1010jiajiao.com/timu3_id_511300[举报]
阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
,β=
代入③得 sinA+subB=2sin
cos
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看习题详情和答案>>
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+subB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
(2012•虹口区一模)已知Sn是数列{an}的前n项和,2Sn=Sn-1-(
)n-1+2(n≥2,n∈N*),且a1=
.
(1)求a2的值,并写出an和an+1的关系式;
(2)求数列{an}的通项公式及Sn的表达式;
(3)我们可以证明:若数列{bn}有上界(即存在常数A,使得bn<A对一切n∈N*恒成立)且单调递增;或数列{bn}有下界(即存在常数B,使得bn>B对一切n∈N*恒成立)且单调递减,则
bn存在.直接利用上述结论,证明:
Sn存在.
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
(1)求a2的值,并写出an和an+1的关系式;
(2)求数列{an}的通项公式及Sn的表达式;
(3)我们可以证明:若数列{bn}有上界(即存在常数A,使得bn<A对一切n∈N*恒成立)且单调递增;或数列{bn}有下界(即存在常数B,使得bn>B对一切n∈N*恒成立)且单调递减,则
| lim |
| n→∞ |
| lim |
| n→∞ |
 是数列
是数列 的前
的前 项和,
项和, (
( ,
, ),且
),且 .
. 的值,并写出
的值,并写出 和
和 的关系式;
的关系式; 有上界(即存在常数
有上界(即存在常数 ,使得
,使得 对一切
对一切 ,使得
,使得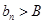 对一切
对一切 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: 存在.
存在.
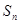 是数列
是数列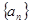 的前
的前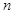 项和,
项和,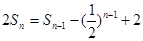 (
(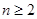 ,
,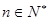 ),且
),且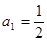 .
.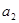 的值,并写出
的值,并写出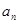 和
和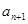 的关系式;
的关系式; 3)我们可以证明:若数列
3)我们可以证明:若数列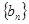 有上界(即存在常数
有上界(即存在常数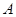 ,使得
,使得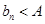 对一切
对一切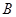 ,使得
,使得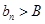 对一切
对一切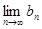 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: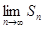 存在.
存在.