题目内容
阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
,β=
代入③得 sinA+subB=2sin
cos
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+subB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
分析:(Ⅰ)把两角和的余项公式减去两角差的余项公式,再把α+β=A,α-β=B代入化简可得结论.
(Ⅱ)利用半角公式以及积化和差公式化简要求的式子,即可求得结果.
(Ⅱ)利用半角公式以及积化和差公式化简要求的式子,即可求得结果.
解答:解 (Ⅰ)证明:因为cos(α+β)=cosαcosβ-sinαsinβ,------①
cos(α-β)=cosαcosβ+sinαsinβ,------②…(1分)
①-②得cos(α+β)-cos(α-β)=-2sinαsinβ.------③…(2分)
令α+β=A,α-β=B,有 α=
,β=
,
代入③得 cosA-cosB=-2sin
sin
.…(5分)
(Ⅱ)sin220°+cos250°+sin20°cos50°=1+
(cos100°-cos40°)+
(sin70°-sin30°)…(8分)
=1-sin70°sin30°+
sin70°-
sin30°=
.…(12分)
cos(α-β)=cosαcosβ+sinαsinβ,------②…(1分)
①-②得cos(α+β)-cos(α-β)=-2sinαsinβ.------③…(2分)
令α+β=A,α-β=B,有 α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)sin220°+cos250°+sin20°cos50°=1+
| 1 |
| 2 |
| 1 |
| 2 |
=1-sin70°sin30°+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题主要考查三角函数的积化和差与和差化积公式的证明,半角公式的应用,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
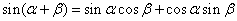 ----------①
----------①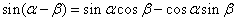 ------②
------②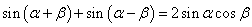 ------③
------③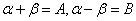 有
有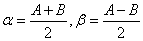
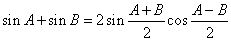 .
. 的值。
的值。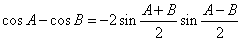 ;
;