题目内容
(15分)已知 是数列
是数列 的前
的前 项和,
项和, (
( ,
, ),且
),且 .
.
(1)求 的值,并写出
的值,并写出 和
和 的关系式;
的关系式;
(2)求数列 的通项公式及
的通项公式及 的表达式;
的表达式;
(3)我们可以证明:若数列 有上界(即存在常数
有上界(即存在常数 ,使得
,使得 对一切
对一切 恒成立)且单调递增;或数列
恒成立)且单调递增;或数列 有下界(即存在常数
有下界(即存在常数 ,使得
,使得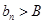 对一切
对一切 恒成立)且单调递减,则
恒成立)且单调递减,则 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: 存在.
存在.
【答案】
(1)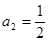 .当
.当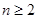 时,
时,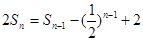 ①;
①;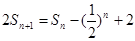 ②
②
②—①得 .又
.又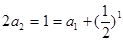 ,即
,即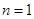 时也成立.
时也成立.
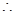

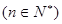 …………………………………………………………5分
…………………………………………………………5分
(2)由(1)得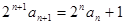 ,
,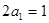 ,
,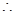
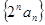 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
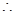
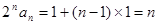 ,
,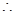
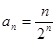 ,
,
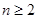 时,
时,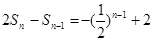 ,
,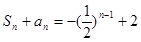 ,
,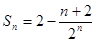 ,
,
又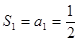 ,也满足上式,
,也满足上式,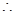
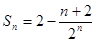
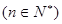 ……………………10分
……………………10分
(3)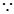
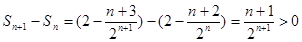 ,
,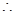
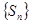 单调递增,
单调递增,
又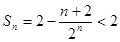 ,
,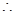
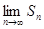 存在……………………………………………15分
存在……………………………………………15分
【解析】略

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
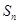 是数列
是数列 的前
的前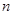 项和,且对任意
项和,且对任意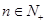 ,有
,有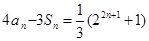 ,
,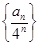 的通项公式;
的通项公式;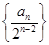 的前
的前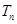 .
.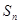 是数列
是数列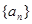 的前
的前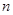 项和,向量
项和,向量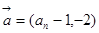 ,
,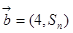 ,且满足
,且满足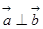 ,则
,则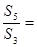
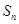 是数列
是数列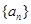 的前
的前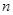 项和,且
项和,且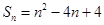
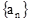 的通项公式;
的通项公式;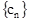 中,所有满足
中,所有满足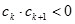 的正整数
的正整数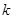 的个数称为这个数列
的个数称为这个数列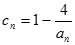 (n为正整数),求数列
(n为正整数),求数列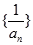 的前
的前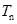 ,若
,若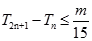 对
对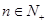 恒成立,求正整数
恒成立,求正整数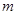 的最小值。
的最小值。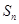 是数列
是数列 的前
的前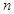 项和,且对任意
项和,且对任意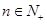 ,有
,有 .记
.记 .其中
.其中 为实数,且
为实数,且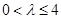 .
.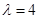 时,求数列
时,求数列 时,若
时,若 对任意
对任意