摘要：如图.平面中两条直线和相交于点.对于平面上任意一点,若分别是到直线和的距离.则称有序非负实数对是点的“距离坐标 .根据上述定义.“距离坐标 是(1.2)的点的个数是 .
网址：http://m.1010jiajiao.com/timu3_id_508872[举报]
16．如图，平面中两条直线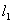
和
相交于点O，对于平面上任意一点M，若
、
分别是M到直线
和
的距离，则称有序非负实数对（
，
）是点M的“距离坐标”．已知常数
≥0，
≥0，给出下列三个命题：
和相交于点O，对于平面上任意一点M，若、分别是M到直线和的距离，则称有序非负实数对（，）是点M的“距离坐标”．已知常数≥0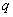，≥0，给出下列三个命题： 
①若
＝
＝0，则“距离坐标”为（0，0）的点有且仅有1个；
②若
＝0，且
＋
≠0，则“距离坐标”为（
，
）的点有且仅有2个；
③若
≠0，则“距离坐标”为（
，
）的点有且仅有4个．
上述命题中，正确命题的个数是 [答]（ ）
（A）0；（B）1； （C）2； （D）3．
查看习题详情和答案>>如图，平面中两条直线
和
相交于点
，对于平面上任意一点
,若
分别是到直线和的距离，则称有序非负实数对
是点的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是____________.
如图，平面中两条直线
和
相交于点
，对于平面上任意一点
,若
分别是到直线和的距离，则称有序非负实数对
是点的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是____________.
查看习题详情和答案>>
和
相交于点
，对于平面上任意一点
,若
分别是
是点
和
相交于点O，对于平面上任意一点M，若
、
分别是M到直线
＝0，且