题目内容

如图，平面中两条直线和相交于点，对于平面上任意一点,若分别是到直线和的距离，则称有序非负实数对是点的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是____________.

4

解析考点：点到直线的距离公式．
分析：若p，q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”，
根据上述定义，“距离坐标”是（1，2）的点，说明M到直线l1和l2的距离分别是1和2，
这样的点在平面被直线l1和l2的四个区域，各有一个点．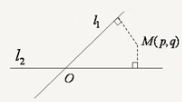

解：如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，
若p，q分别是M到直线l1和l2的距离，
则称有序非负实数对（p，q）是点M的“距离坐标”，
根据上述定义，“距离坐标”是（1，2）的点可以在两条直线相交所成的四个区域内各找到一个，
所以满足条件的点的个数是4个．
故答案为：4．

练习册系列答案
相关题目
12、如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p，q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是
4
．
10、如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p、q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且仅有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（p，q）的点有且仅有2个；
③若pq≠0，则“距离坐标”为（p，q）的点有且仅有4个．
上述命题中，正确命题的个数是（　　）
如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p、q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题①若p=q=0，则“距离坐标”为（0，0）的点有且仅有1个；
②若p=0，q=1，则“距离坐标”为（0，1）的点有且仅有2个；
③若p=1，q=2，则“距离坐标”为（1，2）的点有且仅有4个．
上述命题中，正确命题的个数是（　　）
如图，平面中两条直线l1和l 2相交于点O，对于平面上任意一点M，若x，y分别是M到直线l 1和l 2的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（ p，q） 的点有且只有2个；
③若pq≠0则“距离坐标”为 （ p，q） 的点有且只有3个．
上述命题中，正确的有
①②
①②
．（填上所有正确结论对应的序号）
如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若x，y分别是M到直线l1和l2的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（p，q） 的点有且只有2个；
③若pq≠0则“距离坐标”为 （p，q） 的点有且只有4个．
上述命题中，正确命题的是
①②③
①②③
．（写出所有正确命题的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网