摘要:19.已知函数. (Ⅰ)若关于的方程的解都在区间内.求实数的范围, (Ⅱ)若函数在区间上单调递增.求正实数的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_508634[举报]
已知:函数![]() (
(![]() ),
),![]() .
.
(1)若函数![]() 图象上的点到直线
图象上的点到直线![]() 距离的最小值为
距离的最小值为![]() ,求
,求![]() 的值;
的值;
(2)关于![]() 的不等式
的不等式![]() 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数![]() 的取值范围;
的取值范围;
(3)对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得不等式
,使得不等式![]() 和
和
![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“分界线”。设
的“分界线”。设![]() ,
,
![]() ,试探究
,试探究![]() 与
与![]() 是否存在“分界线”?若存在,求出“分界线”的方程;若不存
是否存在“分界线”?若存在,求出“分界线”的方程;若不存
在,请说明理由.
(A、B选做一题,若两题都做,以A题计分,本题满分14分)
A.已知向量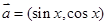 ,
,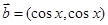 ,
,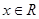 ,函数
,函数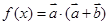
(1)求函数 的最大值与最小正周期;
的最大值与最小正周期;
(2)求使不等式 成立的
成立的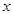 的取值集合.
的取值集合.
(3)若将 向左平移
向左平移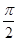 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的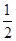 倍得到
倍得到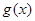 ,关于
,关于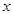 的方程
的方程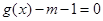 在
在 有且仅有一个解,求
有且仅有一个解,求 的取值范围。
的取值范围。
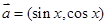 ,
,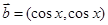 ,
,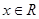 ,函数
,函数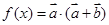
 的最大值与最小正周期;
的最大值与最小正周期;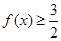 成立的
成立的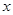 的取值集合.
的取值集合.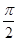 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的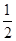 倍得到
倍得到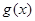 ,关于
,关于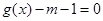 在
在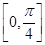 有且仅有一个解,求
有且仅有一个解,求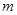 的取值范围。
的取值范围。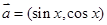 ,
,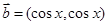 ,
,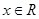 ,函数
,函数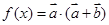
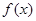 的最大值与最小正周期;
的最大值与最小正周期;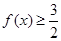 成立的
成立的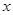 的取值集合.
的取值集合.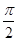 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的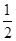 倍得到
倍得到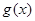 ,关于
,关于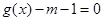 在
在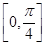 有且仅有一个解,求
有且仅有一个解,求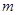 的取值范围。
的取值范围。