题目内容
已知定义域为R的函数 ,且对任意实数x,总有
,且对任意实数x,总有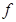 /(x)<3
/(x)<3
则不等式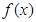 <3x-15的解集为( )
<3x-15的解集为( )
| A.(﹣∞,4) |
| B.(﹣∞,﹣4) |
| C.(﹣∞,﹣4)∪(4,﹢∞) |
| D.(4,﹢∞) |

解析试题分析:设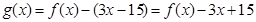 ,则所求的不等式解集可理解为使
,则所求的不等式解集可理解为使 的解集.
的解集.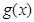 的导函数为
的导函数为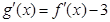 ,根据题意可知
,根据题意可知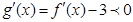 对任意实数
对任意实数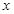 恒成立,所以
恒成立,所以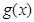 在
在 上单调递减.则
上单调递减.则 ,令
,令 ,则
,则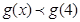 根据单调递减可知:
根据单调递减可知: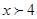 .
.
考点:导数法判断单调性;根据单调性解不等式.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知函数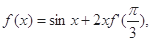 则
则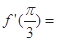 ( )
( )
A.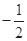 | B. | C.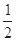 | D.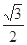 |
设函数 在
在 上的导函数为
上的导函数为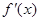 ,
,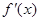 在
在 上的导函数为
上的导函数为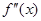 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时,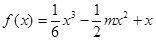 在
在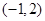 上是“凸函数”.则
上是“凸函数”.则 在
在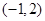 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
已知可导函数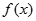 为定义域上的奇函数,
为定义域上的奇函数,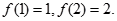 当
当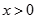 时,有
时,有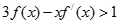 ,则
,则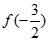 的取值范围为( )
的取值范围为( )
A.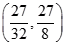 | B.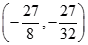 | C.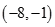 | D.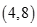 |
直线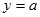 与函数
与函数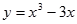 的图像有三个相异的交点,则
的图像有三个相异的交点,则 的取值范围为( )
的取值范围为( )
A.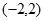 | B.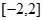 | C.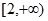 | D.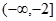 |
设 ,若
,若 ,则
,则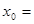 ( )
( )
A.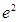 | B. | C.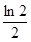 | D. |
在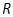 上可导的函数
上可导的函数 的图形如图所示,则关于
的图形如图所示,则关于 的不等式
的不等式 的解集为( ).
的解集为( ).
A. | B. |
C.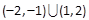 | D. |
函数 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
A.若函数在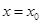 时取得极值,则 时取得极值,则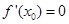 |
B.若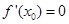 ,则函数在 ,则函数在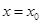 处取得极值 处取得极值 |
C.若在定义域内恒有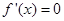 ,则 ,则 是常数函数 是常数函数 |
D.函数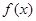 在 在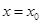 处的导数是一个常数 处的导数是一个常数 |
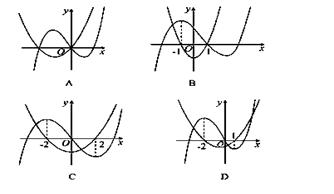
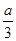 x3+
x3+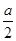 x2-2ax(a≠0)的导函数,则它们的图象可能是 ( )
x2-2ax(a≠0)的导函数,则它们的图象可能是 ( )