摘要：如图.在底面是直角梯形的四棱锥中.AD∥BC.∠ABC＝90°.且.又PA⊥平面ABCD.AD＝3AB＝3PA＝3a. (I)求二面角P-CD-A的正切值, (II)求点A到平面PBC的距离. 解:(1)在底面ABCD内.过A作AE⊥CD.垂足为E.连结PE ∵PA⊥平面ABCD.由三垂线定理知:PE⊥CD ∵∠PEA是二面角P-CD-A的平面角------2分 在中. ------4分 在中. ∴二面角P-CD-A的正切值为------6分 (II)在平面APB中.过A作AH⊥PB.垂足为H ∵PA⊥平面ABCD.∴PA⊥BC 又AB⊥BC.∴BC⊥平面PAB ∴平面PBC⊥平面PAB ∴AH⊥平面PBC 故AH的长即为点A到平面PBC的距离------10分 在等腰直角三角形PAB中..所以点A到平面PBC的距离为
网址：http://m.1010jiajiao.com/timu3_id_500077[举报]
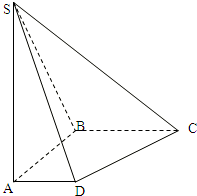如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=| 1 | 2 |
（Ⅰ）求四棱锥S-ABCD的体积；
（Ⅱ）求面SCD与面SBA所成的二面角的正切值． 查看习题详情和答案>>
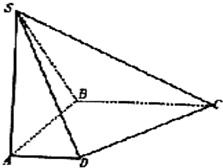如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=2a，AD=a．
（Ⅰ）求点C到平面SBD的距离；
（Ⅱ）求面SCD与面SBA所成的二面角的正切值． 查看习题详情和答案>>
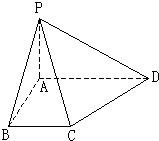如图，在底面是直角梯形的四棱锥P-ABCD中，AD∥BC，∠ABC=90°，且∠ADC=arcsin
| ||
| 5 |
（I）求二面角P-CD-A的正切值；
（II）求点A到平面PBC的距离． 查看习题详情和答案>>
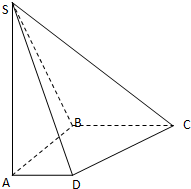如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=
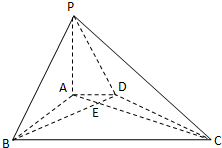如图，在底面是直角梯形的四棱锥 P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，PA=4．AD=2，AB=