摘要:21. [理]已知数列的前三项依次为...前n项和为S n.且Sn=an3+bn2+cn. (Ⅰ)求S n的表达式, (Ⅱ)若数列满足b n=an+1-an.为数列的前n项和.试求使得|-2003|取得最小值的n的值, (Ⅲ)若Tn=.求证:<. [文]如图5.A.B是两个定点.且|AB|=4.动点M到 A点的距离是6.线段MB的垂直平分线交MA于点P. 直线′垂直于直线AB.且B点到′的距离为.若以 AB所在直线为x轴.AB的垂直平分线为y轴建立直角坐标系. (Ⅰ)求证:点P点到点B的距离与到直线′的距离之比为定值, (Ⅱ)若点P到A.B两点的距离之积为m.当m取最大值时.求P点的坐标.
网址:http://m.1010jiajiao.com/timu3_id_498676[举报]
(本小题满分12分)
已知数列{an}的前三项与数列{bn}的前三项对应相等,且a1+2a2+22a3+…+2n-1an=8n对任意的n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得bk-ak∈(0,1)?请说明理由.
 的前三项与数列
的前三项与数列 的前三项对应相同,且
的前三项对应相同,且 对任意的
对任意的 都成立,数列
都成立,数列 是等差数列
是等差数列
 使得
使得 ?请说明理由。
?请说明理由。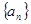 的前三项与数列
的前三项与数列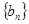 的前三项对应相同,且
的前三项对应相同,且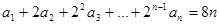 对任意的
对任意的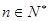 都成立,数列
都成立,数列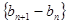 是等差数列
是等差数列
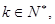 使得
使得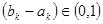 ?请说明理由。
?请说明理由。 ,S3=12+
,S3=12+ .
. ,
, ,…,
,…, ,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
,…成等比数列,其中n1=1,n2=3,求nk(用k表示);