题目内容
(本小题满分12分)
已知数列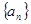 的前三项与数列
的前三项与数列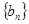 的前三项对应相同,且
的前三项对应相同,且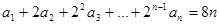 对任意的
对任意的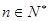 都成立,数列
都成立,数列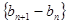 是等差数列
是等差数列
(1) 求数列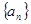 与
与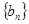 的通项公式;
的通项公式;
(2) 是否存在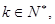 使得
使得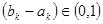 ?请说明理由。
?请说明理由。
已知数列
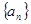 的前三项与数列
的前三项与数列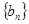 的前三项对应相同,且
的前三项对应相同,且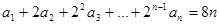 对任意的
对任意的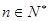 都成立,数列
都成立,数列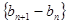 是等差数列
是等差数列
(1) 求数列
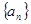 与
与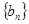 的通项公式;
的通项公式;(2) 是否存在
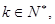 使得
使得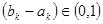 ?请说明理由。
?请说明理由。(1)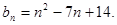 (2)不存在这样的
(2)不存在这样的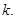
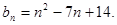 (2)不存在这样的
(2)不存在这样的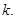
本试题主要是考查了数列的通项公式的求解,以及数列项的关系的比较大小的运用。
(1)因为数列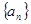 的前三项与数列
的前三项与数列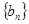 的前三项对应相同,且
的前三项对应相同,且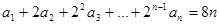 对任意的
对任意的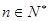 都成立,数列
都成立,数列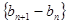 是等差数列利用整体的思想来表示通项公式。
是等差数列利用整体的思想来表示通项公式。
(2)根据上一问中令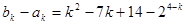 =
=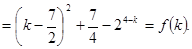
然后结合函数的性质得到函数单调性,进而比较大小得到结论。
(1)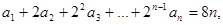
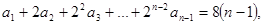
相减,得,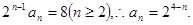
令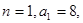 上式也成立,
上式也成立,
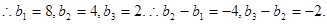
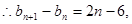 用迭加法可得
用迭加法可得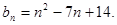
(2)令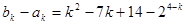
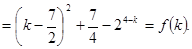
当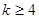 时,
时,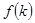 是增函数,
是增函数,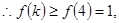
而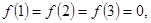 故不存在这样的
故不存在这样的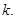
(1)因为数列
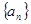 的前三项与数列
的前三项与数列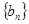 的前三项对应相同,且
的前三项对应相同,且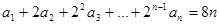 对任意的
对任意的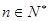 都成立,数列
都成立,数列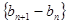 是等差数列利用整体的思想来表示通项公式。
是等差数列利用整体的思想来表示通项公式。(2)根据上一问中令
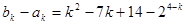 =
=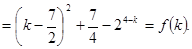
然后结合函数的性质得到函数单调性,进而比较大小得到结论。
(1)
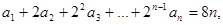
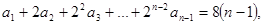
相减,得,
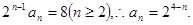
令
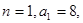 上式也成立,
上式也成立,
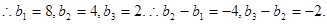
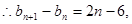 用迭加法可得
用迭加法可得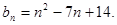
(2)令
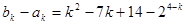
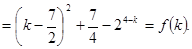
当
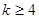 时,
时,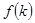 是增函数,
是增函数,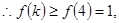
而
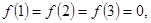 故不存在这样的
故不存在这样的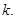

练习册系列答案
相关题目
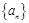 中,
中,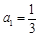 ,且前
,且前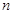 项的算术平均数等于第
项的算术平均数等于第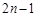 倍(
倍(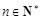 ). (即
). (即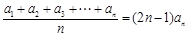
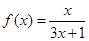 ,数列
,数列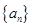 满足
满足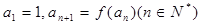 .
.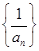 是等差数列,并求数列
是等差数列,并求数列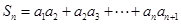 ,求
,求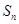 .
.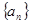 为等比数列,
为等比数列,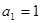 ,
,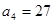 ,
,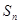 为等差数列
为等差数列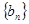 的前
的前 项和,
项和,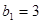 ,
,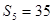 。
。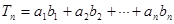 ,求
,求 。
。
 是公差为正数的等差数列,若
是公差为正数的等差数列,若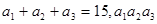 =80,则
=80,则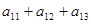 =
=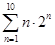 = .
= .