题目内容
（本小题满分12分）如图，直线交
轴于A点，交
轴于B点，过A、B两点的抛物线交
轴于另一点C（3,0）.
⑴ 求抛物线的解析式;
⑵ 在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由.
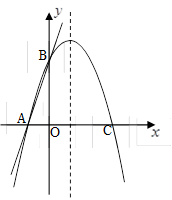
解：（1）设抛物线的解析式为：y=ax2+bx+c。
∵直线交
轴于A点，交
轴于B点，
∴A点坐标为（-1,0）、B点坐标为（0,3）.
又∵抛物线经过A、B、C三点，
∴，解得：
，
∴抛物线的解析式为：y=-x2+2x+3．
（2）∵y=-x2+2x+3=，∴该抛物线的对称轴为x=1．
设Q点坐标为（1，m），则，又
.
当AB=AQ时， ，解得：
，
∴Q点坐标为（1，）或（1，
）；
当AB=BQ时，，解得：
，
∴Q点坐标为（1，0）或（1，6）；
当AQ=BQ时，，解得：
，
∴Q点坐标为（1，1）．
∴抛物线的对称轴上是存在着点Q（1，）、（1，
）、（1，0）、（1，6）、（1，1），使△ABQ是等腰三角形．
解析:略
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
的图象经过A、B两点，根据图中信息解答下列问题：
同侧，在直线
，连接
，与直线
