题目内容
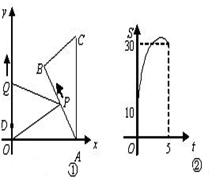
(本小题12分)如图,直线![]() 交
交![]() 轴于A点,交
轴于A点,交![]() 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交![]() 轴于另一点C(3,0).
轴于另一点C(3,0).

1.⑴ 求抛物线的解析式;
2.⑵ 在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
1.解:(1)设抛物线的解析式为:y=ax2+bx+c。
∵直线交
轴于A点,交
轴于B点,
∴A点坐标为(-1,0)、B点坐标为(0,3).
又∵抛物线经过A、B、C三点,
∴,解得:
,
∴抛物线的解析式为:y=-x2+2x+3
2.(2)∵y=-x2+2x+3= ,∴该抛物线的x对称轴为=1.
设Q点坐标为(1,m),则,又
.
当AB=AQ时, ,解得:
,
解析:略

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目


 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交
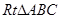 中,
中,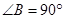
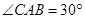 ,
,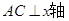 .它的顶点
.它的顶点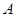 的坐标为
的坐标为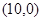 ,顶点
,顶点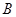 的坐标为
的坐标为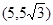 ,点
,点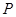 从点
从点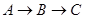 的方向匀速运动,同时点
的方向匀速运动,同时点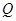 从点
从点 出发,沿
出发,沿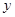 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点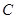 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为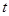 秒.
秒.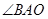 的度数.(直接写出结果)
的度数.(直接写出结果)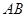 上运动时,
上运动时,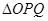 的面积
的面积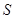 与时间
与时间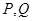 保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.