题目内容
(本题满分10分)如图,直线 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0)
轴于另一点C(3,0) .
.
⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0)
轴于另一点C(3,0) .
. ⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.

解:(1)∵当 =0时,
=0时, =3
=3

当 =0时,
=0时, =﹣1
=﹣1
∴ (﹣1,0),
(﹣1,0), (0,3)
(0,3)
∵ (3,0)··························1分
(3,0)··························1分
设抛物线的解析式为 =a(
=a( +1)(
+1)( ﹣3)
﹣3)
∴3=a×1×(﹣3)
∴a=﹣1
∴此抛物线的解析式为 =﹣(
=﹣( + 1)(
+ 1)( ﹣3)=-
﹣3)=-
 +2
+2 +3·····2分
+3·····2分
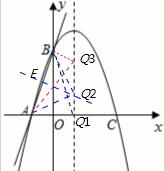
(2)存在∵抛物线的对称轴为:= =1···············4分
=1···············4分
∴如图对称轴与 轴的交点即为Q
轴的交点即为Q
∵ =
=
 ,
, ⊥
⊥

∴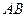 =
=


∴
 (1,0)··························6分
(1,0)··························6分
当

 =
=

 时,设
时,设
 的坐标为(1,m)
的坐标为(1,m)
∴2 +m
+m =1
=1 +(3﹣m)
+(3﹣m)
∴m=1
∴
 (1,1)··························8分
(1,1)··························8分
当

 =
=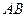 时,设
时,设
 (1,n)
(1,n)
∴2 +n
+n =1
=1 +3
+3
∵n>0 ∴n= ∴
∴
 (1,
(1, )
)
∴符合条件的 点坐标为
点坐标为
 (1,0),
(1,0),
 (1,1),
(1,1),
 (1,
(1, )·10分
)·10分
 =0时,
=0时, =3
=3
当
 =0时,
=0时, =﹣1
=﹣1∴
 (﹣1,0),
(﹣1,0), (0,3)
(0,3)∵
 (3,0)··························1分
(3,0)··························1分设抛物线的解析式为
 =a(
=a( +1)(
+1)( ﹣3)
﹣3)∴3=a×1×(﹣3)
∴a=﹣1
∴此抛物线的解析式为
 =﹣(
=﹣( + 1)(
+ 1)( ﹣3)=-
﹣3)=-
 +2
+2 +3·····2分
+3·····2分
(2)存在∵抛物线的对称轴为:=
 =1···············4分
=1···············4分∴如图对称轴与
 轴的交点即为Q
轴的交点即为Q
∵
 =
=
 ,
, ⊥
⊥

∴
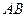 =
=


∴

 (1,0)··························6分
(1,0)··························6分当


 =
=

 时,设
时,设
 的坐标为(1,m)
的坐标为(1,m)∴2
 +m
+m =1
=1 +(3﹣m)
+(3﹣m)
∴m=1
∴

 (1,1)··························8分
(1,1)··························8分当


 =
= 时,设
时,设
 (1,n)
(1,n)∴2
 +n
+n =1
=1 +3
+3
∵n>0 ∴n=
 ∴
∴
 (1,
(1, )
)∴符合条件的
 点坐标为
点坐标为
 (1,0),
(1,0),
 (1,1),
(1,1),
 (1,
(1, )·10分
)·10分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求此时直线PM的解析式;
,求此时直线PM的解析式; ,PM的延长线与CD的延长线交于点F,若三角形G
,PM的延长线与CD的延长线交于点F,若三角形G


 不经过第 象限.
不经过第 象限.
 =____
=____