摘要： 与三角形各边都相切的圆叫做三角形的 .内切圆的圆心是三角形 的交点.叫做三角形的 . [典例精析] 例1 如图.线段 经过圆心 .交⊙O于点 .点 在⊙O上.连接 . ． 是⊙O的切线吗?请说明理由． 例2 如图所示.⊙O的直径AB=4.点P是AB延长线上的一点.过P点作⊙O 的切线.切点为C.连结AC. (1)若∠CPA=30°.求PC的长, (2)若点P在AB的延长线上运动.∠CPA的平分线交AC于点M. 你认为∠CMP的大小是否发生变化?若变化.请说明理由,若不变化.求∠CMP的大小. 例3 如图. 是⊙O的直径. 是⊙O的弦.延长 到点 .使 .连结 .过点 作 .垂足为 ． (1)求证: , (2)求证: 为⊙O的切线, (3)若⊙O的半径为5. .求 的长． 课堂练习
网址：http://m.1010jiajiao.com/timu3_id_466862[举报]
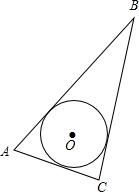与三角形各边都相切的圆叫做三角形的________，内切圆的________叫做三角形的内心．内心到三角形的________相等．如图，⊙O是△ABC的内切圆，△ABC是⊙O的外接三角形．
查看习题详情和答案>>
三角形的内切圆（1）定义：与三角形各边都
相切
相切
的圆叫做三角形的内切圆．内切圆的圆心叫三角形的内心
内心
．（2）三角形的内心是三角形
三角平分线
三角平分线
的交点，它到三角形三边
三边
的距离相等，都等于该三角形内切圆的半径
内切圆的半径
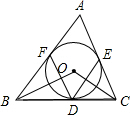
．（3）如图，若△ABC的三边分别为AB=c，BC=a，AC=b，其内切圆⊙O分别切BC、CA、AB于D、E、F．则AF=AE=
| b+c-a |
| 2 |
| b+c-a |
| 2 |
| c+b-a |
| 2 |
| c+b-a |
| 2 |
| a+b-c |
| 2 |
| a+b-c |
| 2 |
∠BOC=90°+
∠A
| 1 |
| 2 |
∠BOC=90°+
∠A
，∠EDF与∠A的关系是| 1 |
| 2 |
∠EDF=90°-
∠A
| 1 |
| 2 |
∠EDF=90°-
∠A
△ABC的面积S与内切圆半径r的关系是| 1 |
| 2 |
r=
| 2s |
| a+b+c |
r=
．| 2s |
| a+b+c |
（4）直角三角形的外接圆半径等于
斜边长的一半
斜边长的一半
，内切圆半径等于面积的2倍与周长的商
面积的2倍与周长的商
．
阅读材料并解答问题：
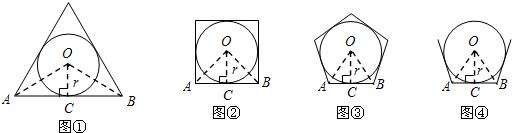
与正三角形各边都相切的圆叫做正三角形的内切圆，与正四边形各边都相切的圆叫做正四边形的内切圆，与正n边形各边都相切的圆叫做正n边形的内切圆，设正n（n≥3）边形的面积为S正n边形，其内切圆的半径为r，试探索正n边形的面积．
（1）如图1，当n=3时，设AB切⊙P于点C，连接OC，OA，OB，
∴OC⊥AB，
∴OA=OB，
∴∠AOC=
∠AOB，∴AB=2BC．
在Rt△AOC中，
∵∠AOC=
•
=60°，OC=r，
∴AC=r•tan60°，∴AB=2r•tan60°，
∴S△OAB=
•r•2r•tan60°=r2tan60°，
∴S正三角形=3S△OAB=3r2•tan60度．
（2）如图2，当n=4时，仿照（1）中的方法和过程可求得：S正四边形=4S△OAB= ；
（3）如图3，当n=5时，仿照（1）中的方法和过程求S正五边形；
（4）如图4，根据以上探索过程，请直接写出S正n边形= ．
查看习题详情和答案>>
与正三角形各边都相切的圆叫做正三角形的内切圆，与正四边形各边都相切的圆叫做正四边形的内切圆，与正n边形各边都相切的圆叫做正n边形的内切圆，设正n（n≥3）边形的面积为S正n边形，其内切圆的半径为r，试探索正n边形的面积．
（1）如图1，当n=3时，设AB切⊙P于点C，连接OC，OA，OB，
∴OC⊥AB，
∴OA=OB，
∴∠AOC=
| 1 |
| 2 |
在Rt△AOC中，
∵∠AOC=
| 1 |
| 2 |
| 360° |
| 3 |
∴AC=r•tan60°，∴AB=2r•tan60°，
∴S△OAB=
| 1 |
| 2 |
∴S正三角形=3S△OAB=3r2•tan60度．
（2）如图2，当n=4时，仿照（1）中的方法和过程可求得：S正四边形=4S△OAB=
（3）如图3，当n=5时，仿照（1）中的方法和过程求S正五边形；
（4）如图4，根据以上探索过程，请直接写出S正n边形=
阅读材料并解答问题：
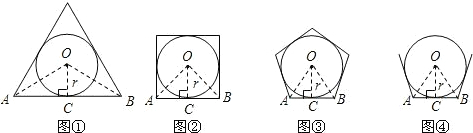
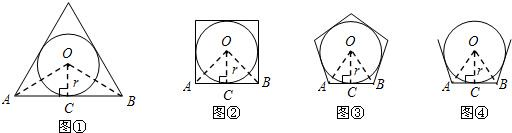
与正三角形各边都相切的圆叫做正三角形的内切圆，与正四边形各边都相切的圆叫做正四边形的内切圆，…，与正n边形各边都相切的圆叫做正n边形的内切圆，设正n（n≥3）边形的面积为S正n边形，其内切圆的半径为r，试探索正n边形的面积．（结果可用三角函数表示）
如图①，当n=3时，设AB切圆O于点C，连接OC，OA，OB，∴OC⊥AB，OA=OB，∴∠AOC=
AOB，AB=2BC．
在Rt△AOC中，∵∠AOC=
•
=60°，OC=r，∴AC=r•tan60°，AB=2r•tan60°，∴S△OAB=
•r•2rtan60°=r2tan60°，∴S正三角形=3S△OAB=3r2•tan60°．
（1）如图②，当n=4时，仿照（1）中的方法和过程可求得：S正四边形= ；
（2）如图③，当n=5时，仿照（1）中的方法和过程求S正五边形；
（3）如图④，根据以上探索过程，请直接写出S正n边形= ．
查看习题详情和答案>>
与正三角形各边都相切的圆叫做正三角形的内切圆，与正四边形各边都相切的圆叫做正四边形的内切圆，…，与正n边形各边都相切的圆叫做正n边形的内切圆，设正n（n≥3）边形的面积为S正n边形，其内切圆的半径为r，试探索正n边形的面积．（结果可用三角函数表示）
如图①，当n=3时，设AB切圆O于点C，连接OC，OA，OB，∴OC⊥AB，OA=OB，∴∠AOC=
| 1 |
| 2 |
在Rt△AOC中，∵∠AOC=
| 1 |
| 2 |
| 360° |
| 3 |
| 1 |
| 2 |
（1）如图②，当n=4时，仿照（1）中的方法和过程可求得：S正四边形=
（2）如图③，当n=5时，仿照（1）中的方法和过程求S正五边形；
（3）如图④，根据以上探索过程，请直接写出S正n边形=
查看习题详情和答案>>
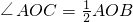，AB=2BC．
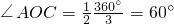，OC=r，∴AC=r•tan60°，AB=2r•tan60°，∴
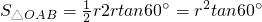，∴S正三角形=3S△OAB=3r2•tan60°．