题目内容
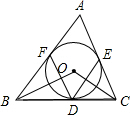 三角形的内切圆
三角形的内切圆(1)定义:与三角形各边都
相切
相切
的圆叫做三角形的内切圆.内切圆的圆心叫三角形的内心
内心
.(2)三角形的内心是三角形
三角平分线
三角平分线
的交点,它到三角形三边
三边
的距离相等,都等于该三角形内切圆的半径
内切圆的半径
.(3)如图,若△ABC的三边分别为AB=c,BC=a,AC=b,其内切圆⊙O分别切BC、CA、AB于D、E、F.则AF=AE=
| b+c-a |
| 2 |
| b+c-a |
| 2 |
| c+b-a |
| 2 |
| c+b-a |
| 2 |
| a+b-c |
| 2 |
| a+b-c |
| 2 |
∠BOC=90°+
∠A
| 1 |
| 2 |
∠BOC=90°+
∠A
,∠EDF与∠A的关系是| 1 |
| 2 |
∠EDF=90°-
∠A
| 1 |
| 2 |
∠EDF=90°-
∠A
△ABC的面积S与内切圆半径r的关系是| 1 |
| 2 |
r=
| 2s |
| a+b+c |
r=
.| 2s |
| a+b+c |
(4)直角三角形的外接圆半径等于
斜边长的一半
斜边长的一半
,内切圆半径等于面积的2倍与周长的商
面积的2倍与周长的商
.分析:(1)直接利用三角形的内切圆的定义写出答案即可;
(2)利用三角形的内心的性质直接写出答案即可;
(3)利用切线长定理和内心的性质直接写出答案即可;
(4)根据前三个题目的解答过程直接写出答案;
(2)利用三角形的内心的性质直接写出答案即可;
(3)利用切线长定理和内心的性质直接写出答案即可;
(4)根据前三个题目的解答过程直接写出答案;
解答:解:(1)与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心叫三角形的内心.
(2)三角形的内心是三角形角平分线的交点,它到三角形三边的距离相等,都等于该三角形内切圆的半径.
(3)如图,若△ABC的三边分别为AB=c,BC=a,AC=b,其内切圆⊙O分别切BC、CA、AB于D、E、F.则AF=AE=
,BD=BF=
,CD=CE=
.∠BOC与∠A的关系是∠BOC=90°+
∠A,∠EDF与∠A的关系是∠EDF=90°-
∠A;△ABC的面积S与内切圆半径r的关系是r=
.
(4)直角三角形的外接圆半径等于斜边长的一半,内切圆半径等于面积的2倍与周长的商.
故答案为:相切,内心;三角平分线,三边,内切圆的半径;
,
;∠BOC=90°+
∠A,∠EDF=90°-
∠A,r=
.斜边长的一半,面积的2倍与周长的商.
(2)三角形的内心是三角形角平分线的交点,它到三角形三边的距离相等,都等于该三角形内切圆的半径.
(3)如图,若△ABC的三边分别为AB=c,BC=a,AC=b,其内切圆⊙O分别切BC、CA、AB于D、E、F.则AF=AE=
| b+c-a |
| 2 |
| c+b-a |
| 2 |
| a+b-c |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2s |
| a+b+c |
(4)直角三角形的外接圆半径等于斜边长的一半,内切圆半径等于面积的2倍与周长的商.
故答案为:相切,内心;三角平分线,三边,内切圆的半径;
| b+c-a |
| 2 |
| c+b-a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2s |
| a+b+c |
点评:本题考查了三角形的内切圆与三角形的内心的关系,牢记这些定义和计算方法是解答本题的关键.

练习册系列答案
相关题目
已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A、1:2:
| ||
| B、2:3:4 | ||
C、1:
| ||
| D、1:2:3 |
下列命题中的真命题是( )
| A、三角形的内切圆半径和外接圆半径之比为2:1 | ||
| B、正六边形的边长等于其外接圆的半径 | ||
C、圆外切正方形的边长等于其边A心距的
| ||
| D、各边相等的圆外切多边形是正方形 |
 如图是某几何体的三视图及相关数据.
如图是某几何体的三视图及相关数据.