题目内容
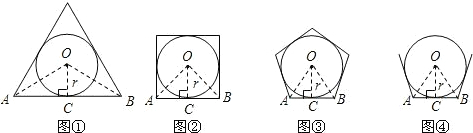
阅读材料并解答问题:与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,…,与正n边形各边都相切的圆叫做正n边形的内切圆,设正n(n≥3)边形的面积为S正n边形,其内切圆的半径为r,试探索正n边形的面积.(结果可用三角函数表示)
如图①,当n=3时,设AB切圆O于点C,连接OC,OA,OB,∴OC⊥AB,OA=OB,∴∠AOC=
| 1 |
| 2 |
在Rt△AOC中,∵∠AOC=
| 1 |
| 2 |
| 360° |
| 3 |
| 1 |
| 2 |
(1)如图②,当n=4时,仿照(1)中的方法和过程可求得:S正四边形=
(2)如图③,当n=5时,仿照(1)中的方法和过程求S正五边形;
(3)如图④,根据以上探索过程,请直接写出S正n边形=
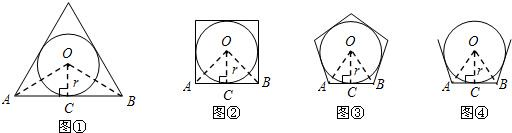
分析:(1)同求正三边的面积的方法一样先计算出中心角∠AOB=90°,在Rt△AOC中,用r表示出AC,然后表示出△OAB的面积,利用S正四边形=4S△AOB计算即可;
(2)同(1)一样,只是中心角=
=72°,得到∠AOC=36°;
(2)同(1)一样,只是中心角=
,得到∠AOC=
.
(2)同(1)一样,只是中心角=
| 360° |
| 5 |
(2)同(1)一样,只是中心角=
| 360° |
| n |
| 180° |
| n |
解答:解:(1)4r2•tan45°;
(2)如图,当n=5时,设AB切⊙O于点C,连接OA,OC,OB,如图,
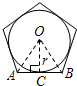 ∵OC⊥AB,OA=OB,
∵OC⊥AB,OA=OB,
∴∠AOC=
∠AOB,AB=2AC,
在Rt△AOC中,∵∠AOC=
•
=36°,OC=r,
∴AC=r•tan36°,AB=2r•tan36°,
∴S△OAB=
•2r•tan36°•r=r2•tan36°,
∴S正五边形=5S△OAB=5r2•tan36°;
(3)nr2•tan
.
(2)如图,当n=5时,设AB切⊙O于点C,连接OA,OC,OB,如图,
 ∵OC⊥AB,OA=OB,
∵OC⊥AB,OA=OB,∴∠AOC=
| 1 |
| 2 |
在Rt△AOC中,∵∠AOC=
| 1 |
| 2 |
| 360° |
| 5 |
∴AC=r•tan36°,AB=2r•tan36°,
∴S△OAB=
| 1 |
| 2 |
∴S正五边形=5S△OAB=5r2•tan36°;
(3)nr2•tan
| 180° |
| n |
点评:本题考查了正多边形的内切圆的性质:圆心到各边的距离相等,都等于圆的半径;也考查了解直角三角形和三角形的面积公式以及正多边形的性质.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目