题目内容
(1)如图,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由。
(2)结论应用:
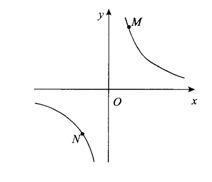
①如图,点M,N在反比例函数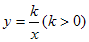 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明:MN∥EF。
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明:MN∥EF。
②若①中的其他条件不变,只改变点M,N的位置,如图所示。请判断MN与EF是否平行。
(2)结论应用:
①如图,点M,N在反比例函数
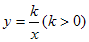 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明:MN∥EF。
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F。试证明:MN∥EF。②若①中的其他条件不变,只改变点M,N的位置,如图所示。请判断MN与EF是否平行。
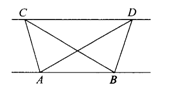
解:(1)证明:分别过点C,D作CG⊥AB,DH⊥AB。垂足为G,H,如图1,
则∠CGA=∠DHB=90°。

图1
∴CG∥DH
∵△ABC与△ABD的面积相等
∴CG=DH
∴四边形CGHD为平行四边形
∴AB∥CD。
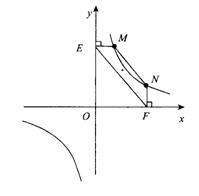
(2)①证明:连结MF,如图2,NE设点M的坐标为(x1,y1),点N的坐标为(x2,y2),
∵点M,N在反比例函数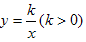 的图象上,
的图象上,

图2
∴x1y1=k,x2y2=k。
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2。
∴S△EFM=x1y1= k。
k。
∴S△EFN=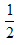 x2y2=
x2y2=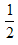 k。
k。
∴S△EFM=S△EEN。
由(1)中的结论可知:MN∥EF。
②如图3所示,MN∥EF。

图3
则∠CGA=∠DHB=90°。

图1
∴CG∥DH
∵△ABC与△ABD的面积相等
∴CG=DH
∴四边形CGHD为平行四边形
∴AB∥CD。
(2)①证明:连结MF,如图2,NE设点M的坐标为(x1,y1),点N的坐标为(x2,y2),
∵点M,N在反比例函数
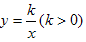 的图象上,
的图象上,
图2
∴x1y1=k,x2y2=k。
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2。
∴S△EFM=x1y1=
 k。
k。∴S△EFN=
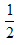 x2y2=
x2y2=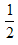 k。
k。∴S△EFM=S△EEN。
由(1)中的结论可知:MN∥EF。
②如图3所示,MN∥EF。

图3

练习册系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=