题目内容
已知一次函数y=kx+b的图象与反比例函数y=-| 8 | x |
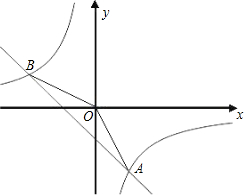 其中A点的横坐标与B点的纵坐标都是2,如图:
其中A点的横坐标与B点的纵坐标都是2,如图:(1)求这个一次函数的解析式;
(2)求△AOB的面积;
(3)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请在坐标轴相应位置上用P1,P2,P3…标出符合条件的点P;(尺规作图完成)若不存在,请说明理由.
分析:(1)因为反比例函数解析式已知,所以把A点的横坐标与B点的纵坐标代入即可求出A点的纵坐标与B点的横坐标,然后代入一次函数解析式中,用待定系数法解答.
(2)在(1)的基础上,可求出一次函数与x轴的交点,利用求和的方法解答.
(3)当OA为腰时,有三个点符合条件,当OA为底时,有一个点符合条件.
(2)在(1)的基础上,可求出一次函数与x轴的交点,利用求和的方法解答.
(3)当OA为腰时,有三个点符合条件,当OA为底时,有一个点符合条件.
解答: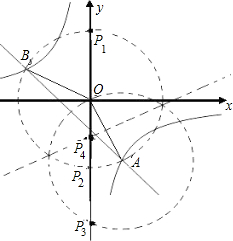 解:(1)反比例函数y=-
解:(1)反比例函数y=-
的图象经过A,B两点,且A点的横坐标与B点的纵坐标都是2;
∴当x=2时,y=-
=-
=-4,把y=2代入y=-
解得:x=-4
∴A点的坐标为(2,-4),B点的坐标为(-4,2);(2分)
∵y=kx+b(k≠0)经过A,B两点;
∴把A(2,-4),B(-4,2)代入y=kx+b(k≠0)得:
解得:k=-1,b=-2;
把k=1,b=2代入y=kx+b(k≠0)得:y=-x-2;(2分)
(2)设直线AB交x轴于点C,把y=0代入y=-x-2解得:x=-2;
∴点C的坐标是C(-2,0);
∴S△AOB=S△BOC+S△OAC=
OC•|YB|+
OC•|YA|
=
OC•(|YB|+|YA|)
=
×2×(2+4)
=6(3分)
(3)如图,P1,P2,P3为所求,它们的坐标分别为:P1(0,2
),P2(0,-2
),P3(0,-8),P4(0,-
).
 解:(1)反比例函数y=-
解:(1)反比例函数y=-| 8 |
| x |
∴当x=2时,y=-
| 8 |
| x |
| 8 |
| 2 |
| 8 |
| x |
∴A点的坐标为(2,-4),B点的坐标为(-4,2);(2分)
∵y=kx+b(k≠0)经过A,B两点;
∴把A(2,-4),B(-4,2)代入y=kx+b(k≠0)得:
|
解得:k=-1,b=-2;
把k=1,b=2代入y=kx+b(k≠0)得:y=-x-2;(2分)
(2)设直线AB交x轴于点C,把y=0代入y=-x-2解得:x=-2;
∴点C的坐标是C(-2,0);
∴S△AOB=S△BOC+S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=6(3分)
(3)如图,P1,P2,P3为所求,它们的坐标分别为:P1(0,2
| 5 |
| 5 |
| 5 |
| 2 |
点评:此题主要考查了一次函数、反比例函数、待定系数法以及等腰三角形的性质等,难易程度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.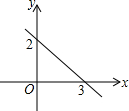 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.