题目内容
(1)探究新知:
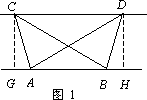
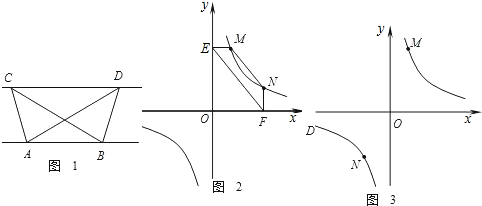
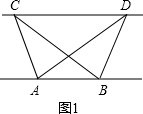
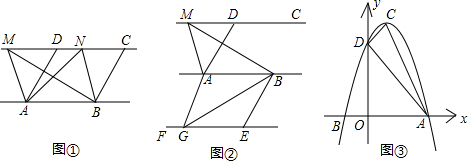
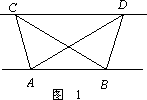
如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
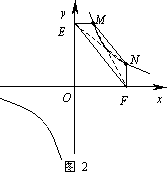
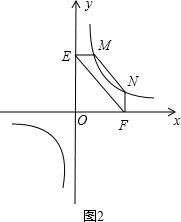
①如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
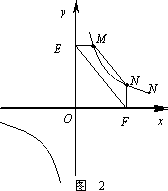
试证明:MN∥EF.
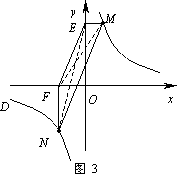
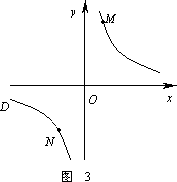
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.
答案:
解析:
解析:
|
(1)证明:分别过点C,D,作CG⊥AB,DH⊥AB,垂足为G,H,则∠CGA=∠DHB=90°. 1分 ∴CG∥DH. ∵△ABC与△ABD的面积相等, ∴CG=DH. 2分 ∴四边形CGHD为平行四边形. ∴AB∥CD. 3分
(2)①证明:连结MF,NE. 4分 设点M的坐标为(x1,y1),点N的坐标为(x2,y2). ∵点M,N在反比例函数 ∴ ∵ME⊥y轴,NF⊥x轴, ∴OE=y1,OF=x2. ∴S△EFM= S△EFN= ∴S△EFM=S△EFN. 7分 由(1)中的结论可知:MN∥EF. 8分
②MN∥EF. 10分
(若学生使用其他方法,只要解法正确,皆给分.) |

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目