摘要：17．如图.四棱锥P -ABCD的底面是矩形.侧面PAD是 正三角形.且侧面PAD⊥底面ABCD.E 为侧棱PD的中点. (1)试判断直线PB与平面EAC的关系, (2)求证:AE⊥平面PCD, (3)若AD = AB.试求二面角A-PC-D的正切值, (4)当为何值时.PB⊥AC ?
网址：http://m.1010jiajiao.com/timu3_id_4471835[举报]
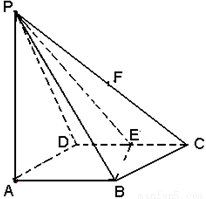
(本题满分14分)．如图所示，四棱锥P－ABCD的底面积ABCD是边长为1的菱形，
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝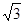
.
(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.
查看习题详情和答案>>
(本题满分14分)．如图所示，四棱锥P－ABCD的底面积ABCD是边长为1的菱形，
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝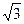
.
(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.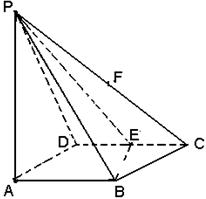
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝
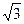.(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.
（本题满分14分）如图，在四棱锥P－ABCD中，PA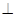
底面ABCD,
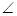DAB为直角，AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
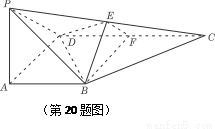
（Ⅰ）试证：CD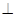平面BEF;
（Ⅱ）设PA＝k·AB,且二面角E-BD-C的平面角大于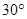
,求k的取值范围.
查看习题详情和答案>>
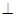底面ABCD,
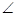DAB为直角，AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.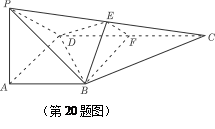
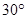,求k的取值范围.
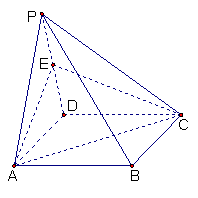⑵若AD=2AB=2,求直线PB与平面ABCD所成角的正切值；
为何值时，PB⊥AC ？