题目内容
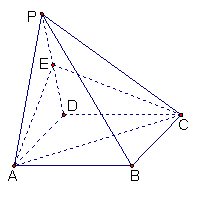
（本题满分14分）如图，四棱锥P －ABCD的底面是矩形，侧面PAD是正三角形，
且侧面PAD⊥底面ABCD，E 为侧棱PD的中点。
⑴求证：PB//平面EAC；
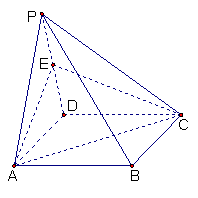⑵若AD=2AB=2,求直线PB与平面ABCD所成角的正切值；
⑶当
为何值时，PB⊥AC ？
（本题满分14分）
解：（1）连结BD交AC于O，连结EO,
因为O、E分别为BD、PD的中点, 所以EO//PB, ……2分
,所以PB//平面EAC。…4分
（2）设N为AD中点，连接PN，则
........5分
又面PAD⊥底面ABCD，所以，PN⊥底面ABCD……………6分
所以
为直线PB与平面ABCD所成的角,…………7分
又AD=2AB=2,则PN=
, ………8分
所以tan=
，即PB与平面ABCD所成角正切为值
。。。。。。9分
（3）由(2)知,NB为PB在面ABCD上的射影,要使PB⊥AC，需且只需NB⊥AC。。。10分
在矩形ABCD中，设AD＝1，AB＝x, 
由
,得
∽
，………………………………………11分
解之得：
, ……………………13分
所以，当
时，PB⊥AC。 …………………………14分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，E是棱CC1上动点，F是AB中点，
；
、
的边长都是1，平面
平面
在
上移动，点
在
上移动，若
（
）
的长；
为何值时，
与面
所成锐二面角余弦值的大小.
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
平面C1CBB1；