题目内容
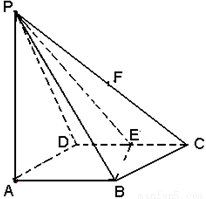
(本题满分14分)．如图所示，四棱锥P－ABCD的底面积ABCD是边长为1的菱形，
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝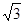
.
(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.
【答案】
略
【解析】解:(Ⅰ)如图所示，连结BD，由ABCD是菱形且∠BCD＝60°知，ΔBCD是等边三角形.因为E是CD的中点，所以BE⊥CD， 2分
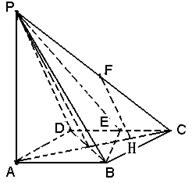又AB∥CD，所以BE⊥AB.又因为PA⊥平面ABCD，
BE
平面ABCD，所以PA⊥BE.而PA∩AB＝A，
因此BE⊥平面PAB.
又BE平面PBE，所以平面PBE⊥平面PAB.
5分
(Ⅱ) 答1：H点在AC线段的4等分点上，且距离C点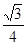
；9分
答2:H点与E点重合 9分
答3：取BC中点G，容易证明平面EFG//平面PBD,那么平面EFG内任意一直线都与平面PBD平行，就是H点在EG直线上都满足题意。
（Ⅲ）由(Ⅰ)知，BE⊥平面PAB，PB平面PAB，所以PB⊥BE.
又AB⊥BE，
所以∠PBA是二面角A－BE－P的平面角. 12分
在RtΔPAB中，tan∠PBA＝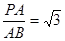
，∠PBA＝60°.
13分
故二面角A－BE－P的大小是60°. 14分
练习册系列答案
阅读快车系列答案
相关题目
为
上的点，且BF⊥平面ACE．
B=[0,3]，求实数m的值
CRB，求实数m的取值范围
是⊙
：
上的任意一点，过
垂直
轴于
,动点
满足
。
，在动点
、
，使
(O是坐标原点)，若存在，求出直线
的方程，若不存在，请说明理由。
.
的定义域；
是否有根?如果有根
，请求出一个长度为
的区间
，使
).