题目内容
(本题满分14分)如图,在四棱锥P-ABCD中,PA 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
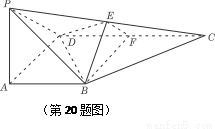
(Ⅰ)试证:CD 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于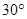 ,求k的取值范围.
,求k的取值范围.
(Ⅰ)见解析;(Ⅱ)k的取值范围为k>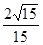
【解析】本试题主要考查了立体几何中线面的垂直的证明以及二面角的求解的综合运用
(1)根据已知的条件,通过线线垂直来判定函数的线面垂直的证明。即由已知DF∥AB且 DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD BF.
BF.
又PA 底面ABCD,CD
底面ABCD,CD AD,故知CD
AD,故知CD PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD
PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD EF,由此得CD
EF,由此得CD 面BEF.
面BEF.
(2)建立合理的空间直角坐标系来表示空间向量的坐标,然后求解法向量,运用法向量的夹角来表示二面角的平面角的大小。
(Ⅰ)解法一:
(Ⅰ)证:由已知DF∥AB且 DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD BF.
………..4分
BF.
………..4分
又PA 底面ABCD,CD
底面ABCD,CD AD,故知CD
AD,故知CD PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD
PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD EF,由此得CD
EF,由此得CD 面BEF. ………..7分
面BEF. ………..7分
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,
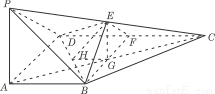
则在△PAC中易知EC∥PA.又因
PA 底面ABCD,故BC
底面ABCD,故BC 底面ABCD.在底面ABCD中,过C作GH
底面ABCD.在底面ABCD中,过C作GH BD,垂足为H,连接EH.由三垂线定理知EH
BD,垂足为H,连接EH.由三垂线定理知EH BD.从而
BD.从而 EHG为二面角E-BD-C的平面角. ………..10分
EHG为二面角E-BD-C的平面角. ………..10分
设AB=a,则在△PAC中,有
BG=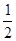 PA=
PA=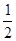 ka.
ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.

因S△CBD=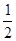 BD·GH=
BD·GH=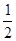 GB·OF.故GH=
GB·OF.故GH=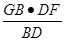 .
.
在△ABD中,因为AB=a,AD=2A,得BD=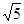 a
a
而GB=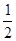 FB=
FB=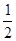 AD-a.DF-AB,从而得GH=
AD-a.DF-AB,从而得GH=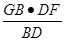 =
=
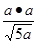 =
=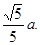 因此tanEHG=
因此tanEHG= =
=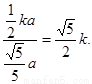 ………..12分
………..12分
由k>0知 是锐角,故要使
是锐角,故要使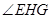 >
>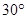 ,必须
,必须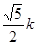 >tan
>tan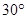 =
=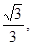
解之得,k的取值范围为k>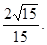 ………..14分
………..14分
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),F(a,2a,0).
从而 =(2a,0,0),
=(2a,0,0), 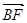 =(0,2a,0),
=(0,2a,0),
 ·
·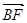 =0,故
=0,故

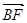
设PA=b,则P(0,0,b),而E为PC中点.故
E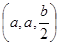 .从而
.从而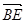 =
=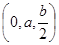 .
.  ·
·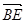 =0,故
=0,故

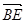 .
.
由此得CD 面BEF.
面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GH BD垂足为H,由三垂线定理知EH
BD垂足为H,由三垂线定理知EH BD.
BD.
从而 EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E ,G(a,a,0).设H(x,y,0),则
,G(a,a,0).设H(x,y,0),则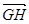 =(x-a,y-a,0),
=(x-a,y-a,0), 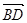 =(-a,2a,0),
=(-a,2a,0),
由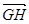 ·
·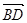 =0得=a(x-a)+2a(y-a)=0,即x-2y=-a
①
=0得=a(x-a)+2a(y-a)=0,即x-2y=-a
①
又因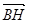 =(x,a,y,0),且
=(x,a,y,0),且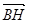 与
与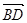 的方向相同,故
的方向相同,故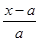 =
= ,即2x+y=2a ②
,即2x+y=2a ②
由①②解得x=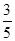 a,y=
a,y=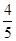 a,从而
a,从而 =
= ,|
,| |=
|=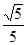 a.
a.
tanEHG=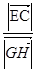 =
=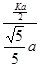 =
=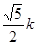 .由k>0知,EHC是锐角,由
.由k>0知,EHC是锐角,由 EHC>
EHC>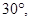 得tanEHG>tan
得tanEHG>tan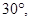 即
即
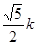 >
>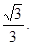 故k的取值范围为k>
故k的取值范围为k>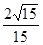

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案

 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;